IIR滤波器的描述和应用技巧

IIR滤波器较FIIR滤波器更为复杂，设计者可以有多种选择来实现。本章中剩余的内容主要讨论和IIR滤波器相关的实现问题。我们知道一个常见的IIR滤波器的差分方程可以表示为

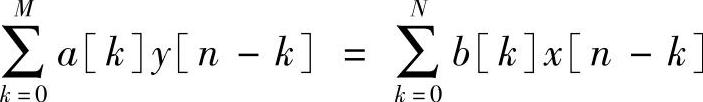
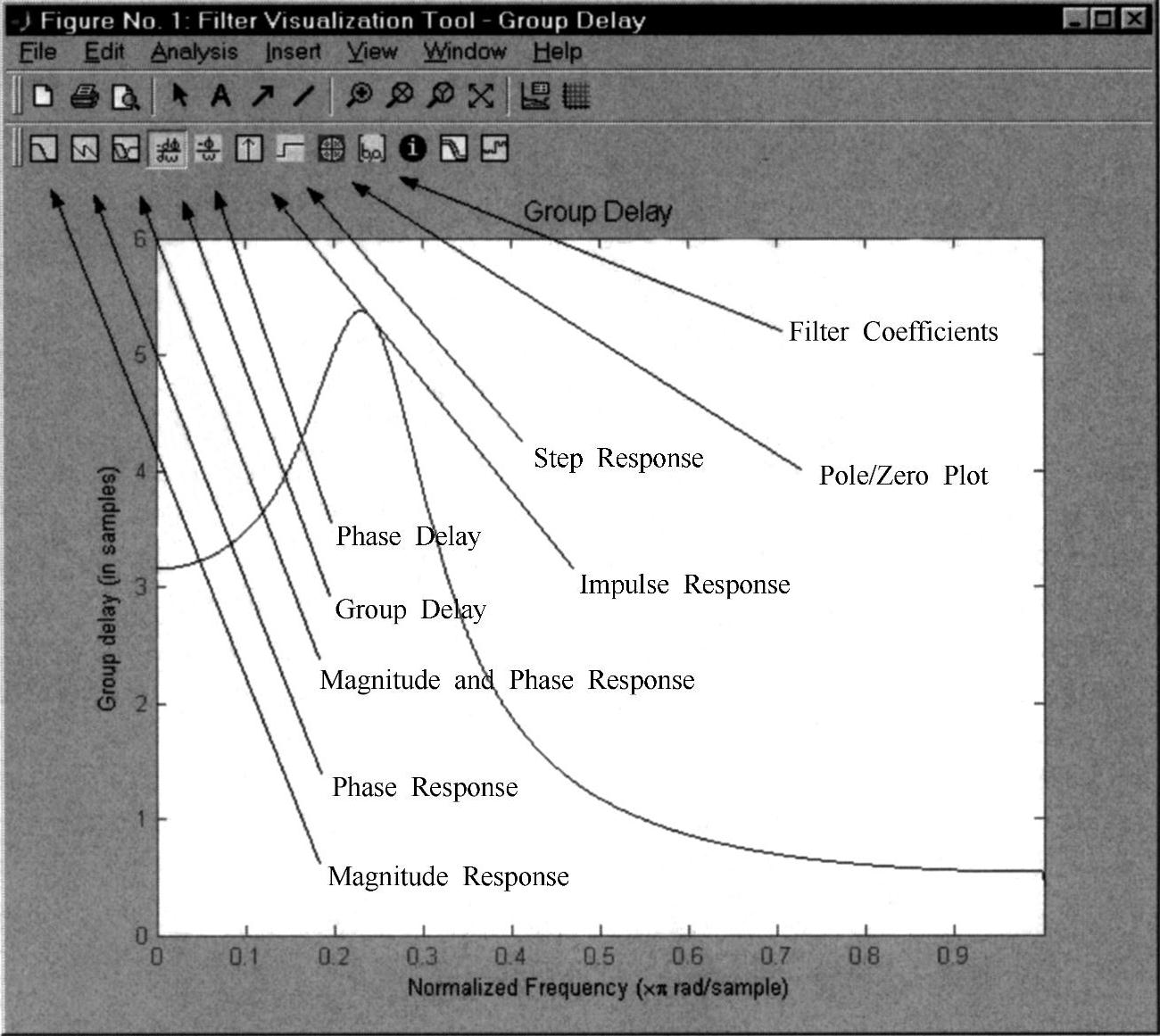
图4.13 FVTool滤波器观察程序的图形用户界面

Filter Coefficients—滤波器系数Pole/Zero Plot—极/零点图Step Response—阶越响应Impulse Reponse—脉冲响应Phase Delay—相位延时Group Delay—群延时Magnitude and Phase

Response—幅度和相位响应Phase Response—相位响应Magnitude Response—幅度响应

或者以输出变量的形式，变为

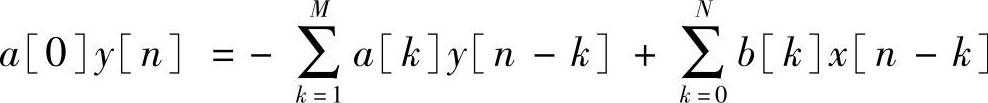
式中每个a[k]和b[k]项目使用a[0]来归一化。我们选择不对上面的差分方程的归一化系数版本重新命名，因为这种形式是普通的DSP教科书中描述IIR滤波器差分方程的通常形式。

或者IIR滤波器的差分方程可以使用z变换的形式描述成如下的传递函数：

(www.xing528.com)

如果我们使用本书第3章所使用的实现一个滤波器相类似的描述方式。上面的传递函数可以变为

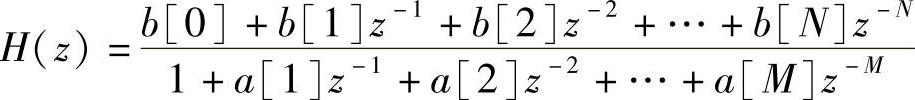
注意，a项的数目为（M+1），b项的数目为（N+1），它们总是不相等的。这就是为什么使用M来表示传递函数多项式的分母的阶数，N表示分子的阶数。

为了计算y[0]（IIR滤波器的当前输出数值），我们进行下面两步计算：

（1）点乘B·x，其中B={b[0]，b[1]，…，b[N]}，x={x[0]，x[-1]，…，x[-N]}（输入信号的当前和过去的数值）。

（2）点乘A·x，其中A={1，a[1]，…，a[M]}y={y[0]，y[-1]，…，y[-M]}（输出信号的当前和过去的数值）。特别地有

y[0]=-a[1]y[-1]-a[2]y[-2]-…-a[M]y[-M]+b[0]

x[0]+b[1]x[-1]+…+b[N]x[-N]

注意，A·y项是一个部分的点乘。因为不需要a[0]y[0]项目从而不需要对其进行计算。