如先前提到的,Matlab有一个内建的函数叫filter.m。这个函数既能够用于实现FIR滤波器(只用分子(B)的系数)又能够用于实现IIR滤波器(用分母(A)和分子(B)的系数)。和滤波器相关的在线帮助命令如下所列。在命令行中通过键盘输入Matlab的帮助命令也是可以的,格式如下。
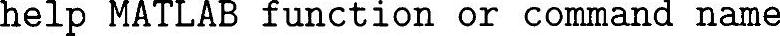
滤波器命令如下。

注意,在讨论的Matlab命令的差分等式中,系数矢量A和B的索引号从1开始而不是从0开始。Matlab不允许索引号等于0。在Matlab算法开发过程中,计算一个有符号数的误差不合适的矢量索引号将带来一些不便。在我们的课程中,我们产生一个典型的矢量“n”,它包含的第一个整数元素等于0。例如,“n=0:15”指n={0,1,2,3,…,15。并且使用这个矢量“n”来“欺骗”Matlab从零开始在坐标轴上开始画图。下面的代码,就是使用这项技术的例子。
如下所示的Matlab代码将使用系数为矢量B的FIR滤波器来对输入矢量x进行滤波。注意,在输入矢量x中添0直到与滤波器一致。这个方法不同于直接使用Matlab的滤波器命令(这里对于M个输入值将有M个输出值)。我们的方法确保输入矢量的前后都有许多零。这意味着滤波器起初是静止的(没有初始条件),并且在滤波运算结束的时候将放宽或清除任何残余值。
程序清单3.1:在Matlab中简单的FIR滤波器例子

对于这个例子的输出如下。
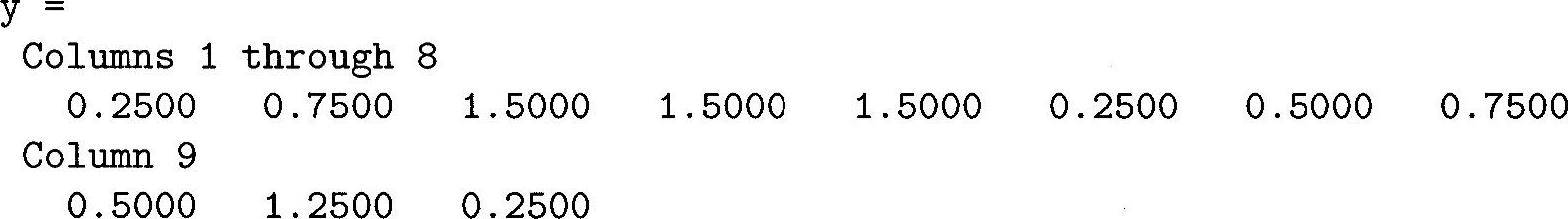
例子的火柴棍型图如图3.12所示。
在这个例子中,8个输入采样点被滤波并且结果全部立即返回。注意,当8元素的矢量x被4元素矢量B滤波时将输出11个元素(8+4-1=11)。x和B进行卷积(滤波)后的结果序列长度是L=序列(x)长度+序列(B)长度-1。
这个FIR滤波器系数是B=[0.250.250.250.25]。因为这个滤波器有4个系数,这是一个3阶滤波器(即N=3)。在此情况下,滤波器的作用是对最近的4个输入采样值求平均值(即当前的采样值和以前的3个采样值求平均)。这类滤波器称为滑动平均(Moving Average,MA)滤波器,并且是一种低通FIR滤波器。图3.13所示为滑动平均滤波器的频率响应,滤波器的阶数N=3、7、15、31,采样频率是48kHz。
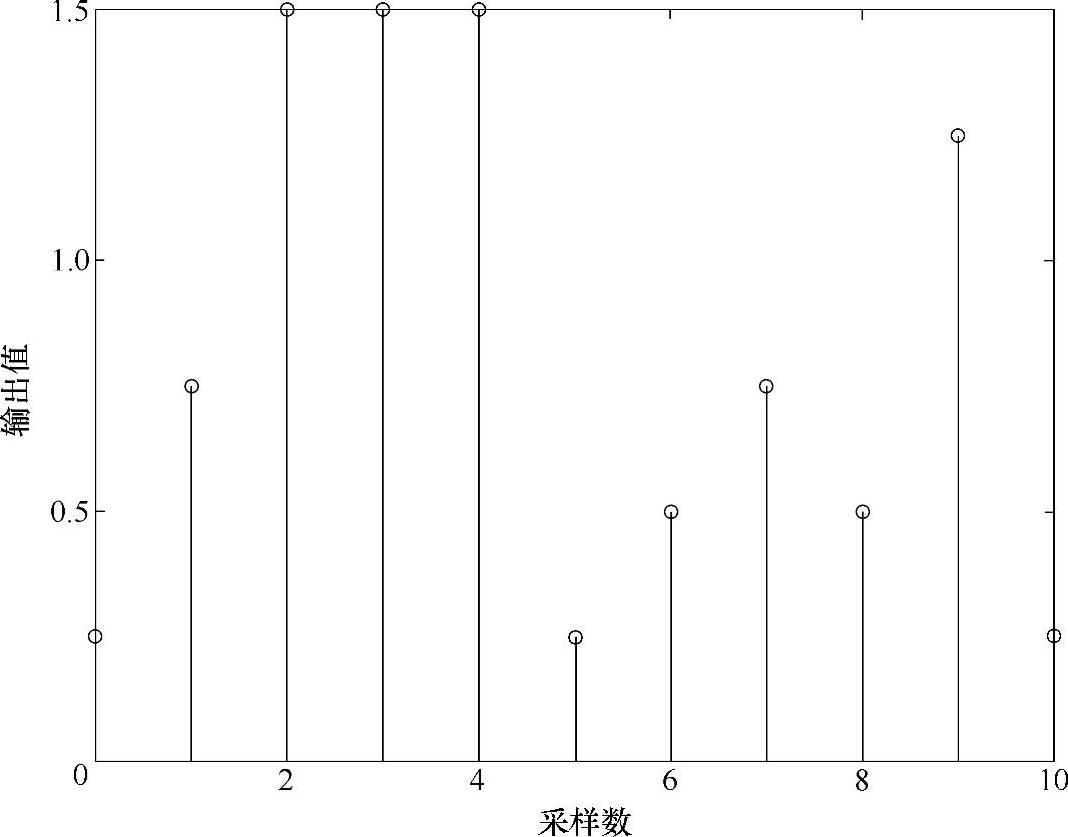
图3.12 用矢量B对x滤波后输出的火柴棍型图
 (https://www.xing528.com)
(https://www.xing528.com)
图3.13 阶数为3、7、15、31的滑动滤波器的频率响应曲线
上述各阶数的滑动平均滤波器频率响应曲线如图3.13所示,在0Hz(直流)处的增益值是1(等于0dB)。为确保任何滤波器的直流增益为0dB,脉冲响应h[n]的和必须等于1。直流响应和脉冲响应的关系,能够很快通过用h[n]描述的一个因果系统z变换表示出来:

为了变换H(z)到频率响应H(ejω),必须使用可变的替代式z=ejω[10],替换后变为
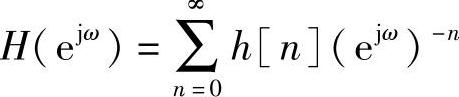
为了评估N阶滤波器的直流响应,设ω=0并且求和的上限等于N。结果为
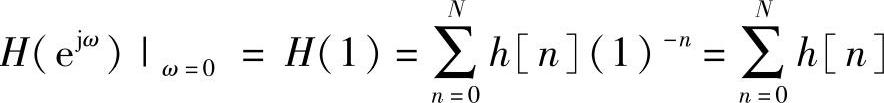
这个关系式解释了为什么对于N=3时,与MA滤波器相关的4个h[n]项就确定为1/4=0.25。类似地,对于N=31,每一个项h[n]将是1/32=0.03125,从而保证直流响应等于1(即0dB)。
一个实际的滤波例子
有无限多的数据集或者处理进程能够被滤波处理。比如,如果我们想要知道股票市场4天或者32天的收盘值的均值是多少?如果这个收盘值经过了滤波处理,许多日复一日的市场变化值被移走。滤波器的截止频率用于滤除这个收盘值将控制剩余变量的数量。如图3.13所示,对于一个滑动平均滤波器,其截止频率是与滤波器的阶数逆相关。图3.14所示为滤波和未滤波的2001年的纳斯达克(National Association of Securities Dealers Automated Quotations,NASDAQ)综合指数的收盘值。
这个图的上半部分画出了原始数据和使用MA滤波器对原始数据进行4-项(3阶)及32-项(31阶)滤波处理的结果。这个子图是使用Matlab中的filtfilt函数生成的。这个函数使用了一个零相位前向和翻转滤波器(即零群延迟)。这个前向/翻转技术用于消除群延迟而不能用于实时滤波。对于Matlab中的filtfilt函数附加信息,可以从Matlab命令中输入help filtfilt获得提示。
这个图的下半部分画出了原始数据和使用MA滤波器对原始数据进行4-项(3阶)及32-项(31阶)滤波处理的结果。这个子图是使用Matlab中的filter函数。因为意识到MA滤波器有一个非零的群延迟。滤波后数据相对于原始数据的延迟时间等于群延迟GD乘以采样周期Ts。
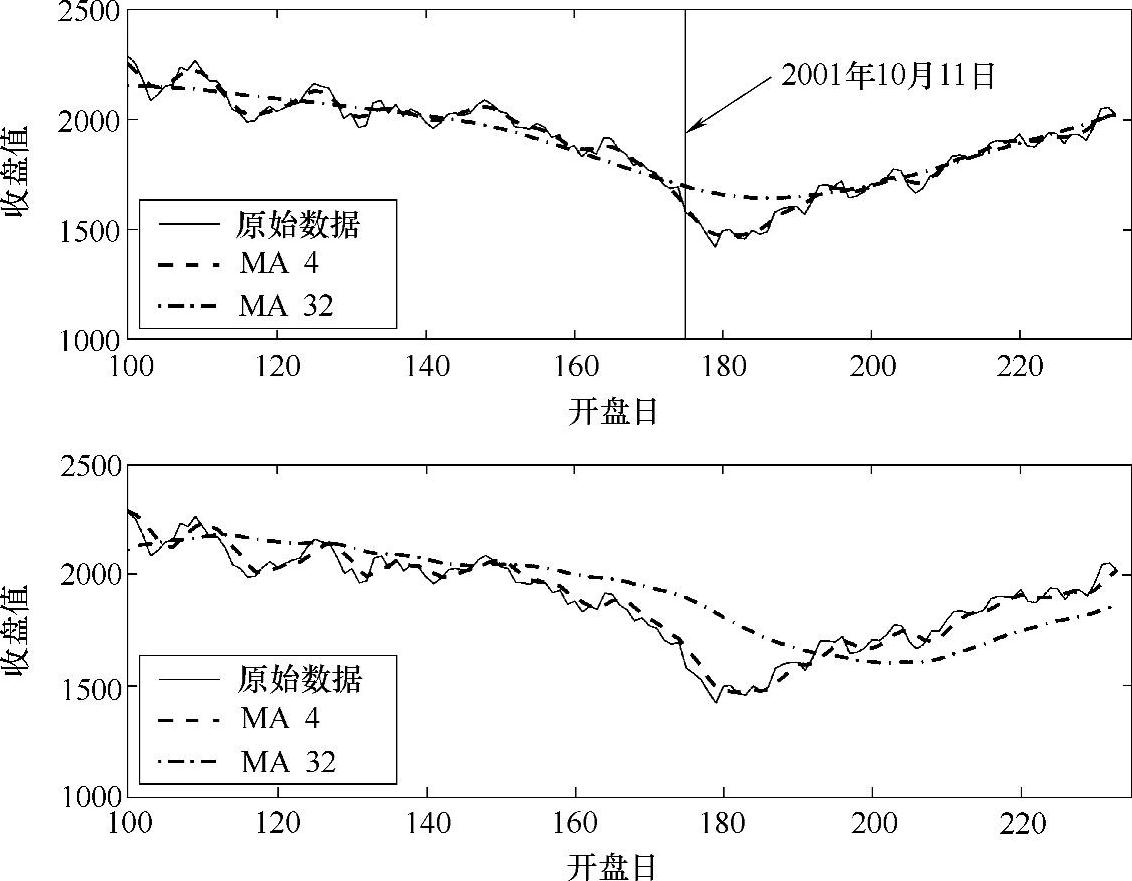
图3.14 滤波和未滤波的2001年纳斯达克(NASDAQ)综合指数的收盘值
注:上图用Matlab中的filtfilt函数生成,下图用Matlab中的filter函数生成。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




