为了计算一个连续时间系统的输出，一个连续时间输入信号已经加载到这个系统上，我们需要把输入信号和系统的脉冲响应函数进行卷积。因为这个卷积是连续信号，我们用积分方法（离散信号用求和代替积分）。因而为计算输出我们需要计算卷积值。这是一个令许多初学者感到神秘和困难的运算过程（然而习惯于使用卷积———这一点一再被提及）。
一般的卷积形式为
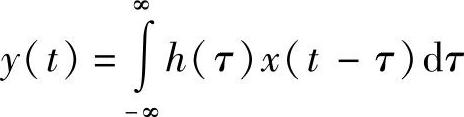
如果我们把讨论限定在可实现的信号和系统范围内，也就是因果系统（比如，我们计算不出输入信号到达以前的系统输出）卷积变为
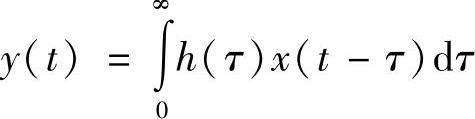
同样地，为计算离散时间系统的输出，输入信号也是离散时间信号，我们使用卷积求和。通常的卷积求和形式为
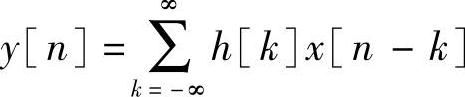
如果再次将讨论限定在可实现的信号和系统范围内，那么因果系统的卷积求和变为
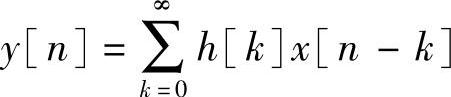(www.xing528.com)
对一个有限冲激响应FIR系统，构成系统脉冲响应的滤波器系数项是独立的。滤波器系数通常称为b项系数。在Matlab中，当全部的b项系数构成一个矢量，称为矢量B。做一个代替（用b代替h）并且牢记一个N阶FIR滤波器有N+1项系数，卷积求和表现为FIR差分等式的常见形式为
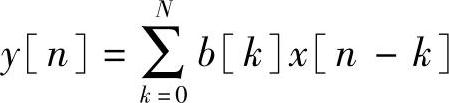
这一等式告诉我们为了计算当前输出值，y[0]，我们必须执行点乘B·X。这里B={b[0]，b[1]，…，b[N]}，并且X代表输入信号的当前值和过去值，X={x[0]，x[-1]，…，x[-N]}即是
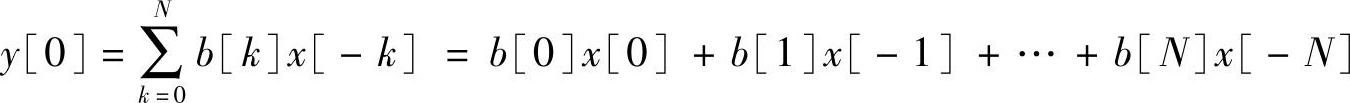
下面的框图说明的是FIR差分关系式实现，也是FIR滤波器的另一种表述形式，如图3.2所示。框图中包含z-1的是延迟项，存储的是前一个采样周期的值。延迟框可以看作是同步移位寄存器，移位时钟依赖于ADC采样时钟或者DAC的转换时钟，而且比较有代表性的存储器位于DPCPU上。
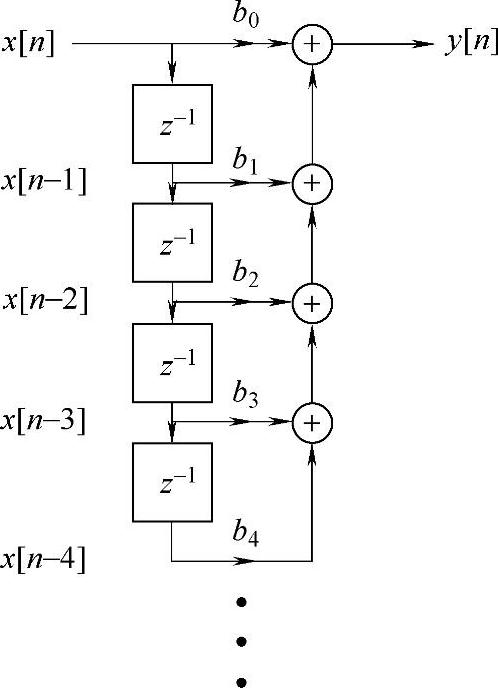
图3.2 与FIR滤波器实现有关的结构框图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
