均质炸药的冲击起爆机理探究

均质炸药指物理结构均匀，内部没有气泡和杂质，具有均一物理和力学性质的炸药，如硝化甘油液体、太安单晶体等。均质炸药冲击起爆，一般认为是冲击波进入炸药后，波阵面后首先受到冲击的一层炸药被整体加热，发生化学反应，并形成超速爆轰过程，对应的超速爆轰波追赶上初始入射波后，在未受冲击的炸药中发展成稳定爆轰。这种均质炸药的冲击起爆模型是由Campbell等人基于实验提出的，在对应的液态硝基甲烷冲击起爆实验中，通过扫描摄影发现，冲击波进入液态硝基甲烷一定时间后，受到冲击压缩的硝基甲烷中产生了微弱的辉光，并在某一时刻后转变为强烈爆轰发光。该现象表明，辉光区相伴随的高速扰动，对应冲击压缩后硝基甲烷的爆轰。

根据流体力学模型，预压缩炸药爆速大于正常炸药爆速。若将超速爆轰波假设为稳定波，可以得到均质炸药冲击起爆行波规律，如图5.1所示。图中，线1为初始冲击波轨迹，速度为DI；线2为冲击波阵面后炸药质点运动轨迹，速度为u；线5为超速爆轰波轨迹，速度为D′；线6为正常爆轰波轨迹，速度为D；3为炸药表面热爆炸延迟时间；4为超速爆轰波后弱辉光时间。

图5.1　均质炸药冲击起爆行波图

此外，研究表明，起爆延迟时间对初始冲击波压力、炸药温度、纯度很敏感。当冲击压力由8.6 GPa增加到8.9 GPa时，延迟时间从2.26 μs减少到1.74 μs，温度由1.6℃升高到26.8℃时，延迟时间由5.0 μs减少到1.8 μs。同时，起爆深度（炸药中爆轰点距炸药界面的距离）也受初始冲击波压力和炸药温度影响，初始冲击波压力低于10 GPa时，起爆位置逐渐移向炸药内部，且当入射压力低于某临界值时，炸药不再起爆，该值即为临界起爆压力。

苏联学者基于热爆炸理论，对均质炸药冲击起爆特征参量进行了计算。均质炸药冲击起爆延迟时间τ与温度T存在下述关系

式中，ρ为炸药密度；cp为炸药恒压比热容；R为普适气体常数；Q为炸药爆热；E为活化能；k0为与反应速率相关的常数；T为波后炸药温度。

温度T可通过冲击波阵面上压力计算获得，若采用炸药晶体状态方程，并结合能量守恒方程，可计算冲击波阵面后的温度，表述为

式中，p为冲击压力；V0为炸药初始体积；V为任意时刻炸药体积；pT为炸药冲击起爆压力；T0为初始温度；cV为炸药恒容比热容。

根据Gruneisen状态方程，同一体积V处，冲击绝热曲线上一点（p，V）和等温线上一点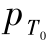（，V）间的关系为

对式（5.2）进行微分，并将式（5.3）代入，取T0=0，得

式中，Γ为Gruneisen系数。式（5.4）为冲击波阵面后温度T的一阶常微分方程，求解该式得

式中，p（V）可以依据炸药冲击绝热线线性关系获得

式中，c0为介质中声速；λ为与材料有关的常数。(www.xing528.com)

Gruneisen系数Γ为

或者由下式求出

式中，α为膨胀系数；KT为等温体积模量；cb为流体力学声速；Γ0为初始Gruneisen系数。

恒压比热容cV可由德拜公式计算获得

式中，R为普适气体常数；μ为摩尔质量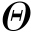；为德拜温度。令，则有

当，此时cV=3R/μ。

在此基础上，苏联学者基于表5.1所列均质炸药常数，计算得到了8种均质炸药的起爆压力pr和延迟时间τ，列于表5.2。

表5.1　均质炸药常数

续表

注：β0为炸药体积膨胀系数。

表5.2　均质炸药起爆数据