薄靶爆裂增强模型优化

薄铝靶在活性弹丸侵彻作用下，形成典型花瓣形破坏，毁伤参数描述如图2.46所示。其中，δ为侵孔隆起高度，Dc为侵孔直径。活性弹丸碰撞薄铝靶实验中侵孔隆起高度、侵孔直径统计结果列于表2.8。可以看出，弹丸碰撞速度在289～569 m/s范围内时，侵孔直径和隆起高度显著受碰撞速度影响。

进一步分析活性弹丸动能和爆炸化学能联合作用下铝靶变形量与弹靶作用条件的关系，引入靶板隆起高度δ与弹靶参数的关系可表述为

式中，分别为碰撞载荷有效作用时间和化学反应载荷有效作用时间；为碰撞载荷平均作用压力；为爆燃反应平均作用压力；C1和C2为与靶板材料有关的常数；ρt为靶板密度；h为靶板厚度。

图2.46　碰撞薄铝靶毁伤参数描述

表2.8　碰撞3 mm靶实验结果

研究表明，弹靶碰撞过程产生的压力正比于碰撞速度的平方。假设碰撞压力有效作用时间表述为

式中，vi为侵彻速度；Lp为弹丸长度。考虑到侵彻速度和碰撞速度之间存在线性关系，则平均碰撞压力和压力有效作用时间可表述为

式中，v为碰撞速度；B和B′为常数。

将式（2.88）代入式（2.86），得到铝靶隆起高度

式中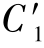，为常数，与常数C1、B、B′的关系为

给定靶板厚度、密度以及活性毁伤材料弹丸长度条件下，通过式（2.89），可获得铝靶相对隆起高度

式中，δ（v）为碰撞速度v时铝靶隆起高度；δ（v0）为碰撞速度v0时铝靶隆起高度；根据式（2.89）～式（2.91），得到f（v0）表达式(www.xing528.com)

在给定碰撞速度v0和弹丸长度条件下，可认为f（v0）为常数，于是可得

对式（2.92）右边第一项分子和分母同时除以v0可以得到

从式（2.93）中可以看出，给定弹丸长度和碰撞速度v0条件下，式中右边两项参数大多为常数，于是，为便于问题分析，令

于是，式（2.93）可简化表述为

式中，C3和C4为常数，取值由靶板厚度、密度、弹丸长度和碰撞速度决定。

在式（2.94）中，右侧第一项表征碰撞载荷对隆起高度的影响，第二项反映化学反应载荷对隆起高度的影响。由于式中系数及f（v）难以通过理论分析得到，假设f（v）为v/v0的一次函数，则在碰撞速度为289～482 m/s范围内，基于表2.8所列实验数据，通过拟合可获得相对隆起高度随碰撞速度的经验关系式，拟合曲线如图2.47所示。根据拟合方程，得到经验关系式为

图2.47　相对隆起高度数据拟合

需要注意的是，式（2.95）中第一项系数1.42并非系数C3取值，而是右边两项共同作用之后的一次项系数。忽略活性弹丸侵彻过程中化学反应载荷作用，即忽略式（2.91）中f（v）和f（v0）项，可得相对隆起高度为

通过式（2.95）～式（2.96）和表2.8所示实验数据得到活性弹丸作用下铝靶隆起高度和碰撞速度关系如图2.48所示，其中v0取值为289 m/s。可以看出，碰撞速度为289～482 m/s时，随碰撞速度v增大，相对隆起高度δ（v）/δ（v0）呈增大趋势。进一步分析还可看出，相对隆起高度实验值始终大于式（2.96）计算结果，且二者间差值随碰撞速度提高呈增大趋势。但当碰撞速度为569 m/s时，相对隆起高度实验值却显著低于式（2.96）计算值。

图2.48　碰撞速度对隆起高度影响

在活性弹丸碰撞作用下，铝靶相对隆起高度随碰撞速度变化所呈现的独特规律，可从以下方面进行分析。首先，从式（2.86）可以看出，隆起高度决定于碰撞载荷和化学能释放载荷的联合作用，而式（2.96）计算结果忽略了化学能释放载荷的作用，因此，二者存在较大差异。其次，随着碰撞速度从289 m/s增大至482 m/s，活性材料激活反应率提高，导致侵彻过程中更多活性材料激活释放化学能，显著增强了化学响应对铝靶的结构毁伤作用，从而导致实验值显著高于式（2.96）计算结果，且二者差值随碰撞速度的提高呈逐渐增大趋势。但是，当碰撞速度增大至569 m/s时，由于碰撞压力的急剧增大，导致铝靶在碰撞接触面轴向发生断裂，中断了能量从碰撞点沿靶板周围的传播，阻止了径向裂纹的传播，从而使得实验值明显低于式（2.96）计算结果，铝靶也不再呈现明显的花瓣形破坏。也就是说，在289～482 m/s速度范围内，随着碰撞速度增大，活性材料在侵彻过程中的化学响应对毁伤效应的影响显著增强，在一定程度上提高了活性弹丸对铝靶的毁伤能力。