弹道速度的极限值是多少？

弹丸侵彻目标时，利用动能在目标内开辟通道，弹丸能否穿透目标，取决于弹丸的贯穿能力，常通过弹道极限速度衡量。弹道极限速度是指弹丸以规定的着靶姿态，贯穿给定靶板所需的碰撞速度。实际上，对于给定的弹丸和靶标，弹道极限速度反映了在规定条件下弹丸贯穿靶板所需的最小动能。

常用弹道极限速度有三种，分别为陆军弹道极限速度、防御弹道极限速度、海军弹道极限速度，如图2.5所示。美国陆军弹道极限标准规定，弹道极限速度是弹丸可刚好贯穿靶板，靶后无飞散碎片所需的最低速度。防御弹道极限速度指弹丸穿透装甲，且可在靶后产生满足要求的动能碎片所需的最低速度。海军弹道极限速度，是指弹丸完全穿过装甲板所需的最低速度。

对一组特定弹丸和目标，弹道极限速度并非固定值，而是一段速度区间，如图2.6所示。随弹丸速度增加，贯穿率分为三个区间。当着速v小于某一速度v1时，所有弹丸均不能贯穿靶板，对应非贯穿区（1）；当v大于速度v2时，弹丸均能贯穿靶板，对应贯穿区（3）。当v在v1与v2之间时，弹丸可能贯穿目标，也可能不贯穿，贯穿百分比随弹丸速度的提高而增加，对应临界区（2）。其中，50％和90％概率贯穿时对应弹道极限速度分别称为v50和v90，对应的标准方差分别表示为σ50和σ90。v50和v90越小表明弹丸贯穿能力越强，σ50和σ90越小表明弹丸贯穿性能越稳定。v90和v50间关系经验公式表述为

图2.5　三种弹道极限速度

图2.6　贯穿率随着速变化关系

弹道极限速度常通过“升降法”实验获得。实验中，首先按弹/靶作用条件对弹道极限速度进行初步估算；然后按弹丸质量、发射药量与发射初速经验关系，确定发射药量和发射弹丸质量，并根据所测弹丸速度和靶板穿孔状态，按“升降法”调整发射药量和发射初速。若弹丸贯穿靶板，则减少发射药量再次实验，若弹丸未贯穿靶板，则增加发射药量，提高发射速度，再次实验。实验后，依据实验结果及数据处理方法，给出弹道极限速度。

依据不同实验方法、弹靶材料特性、弹靶作用条件、弹道侵彻实验结果，弹道极限速度可通过经验公式、理论分析获得。

低速条件下，弹丸依靠动能击穿目标。弹丸击穿目标所需能量，应不小于目标动态变形功

式中，Eim和E分别为弹丸贯穿目标所需能量和目标动态变形功，且

式中，K1为比例系数，取决于材料性质；As为弹丸作用于靶板的面积；b为靶板厚度；σb为靶板强度。

一般来说，不同厚度、强度材料靶板可相互进行等效，等效关系可表述为

式中，b、bA1分别为待等效靶板和已知靶板的厚度；σ、σA1分别为待等效靶板和已知靶板的材料强度。由式（2.4）和式（2.3）有

弹丸击穿厚度为bA1的靶板时，撞击能必须满足

即

弹丸作用靶板单位面积比能Eam可表述为

式中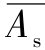，为弹丸作用于靶板的平均面积；Eb为衡量贯穿作用的参数。当弹丸侵彻过程中作用于靶板的比能低于靶板变形功时，则无法贯穿靶板。当Eb＜E时，则击穿概率PMe为0；当Eb＞E时，则击穿概率PMe为1。

美国弹道研究实验室（Ballistic Research Laboratory）通过对多种材料及形状弹丸侵彻实验数据的统计拟合，提出了THOR方程，适用于估算弹丸低速碰撞侵彻时的剩余速度和剩余质量。剩余速度表述为

式中，Ms、Vr、Vs分别为弹丸质量、剩余速度和碰撞速度；e为靶板厚度；A为弹丸侵彻区域面积；θ为弹丸入射方向和靶板法线间的夹角；c、α、β、γ、λ均为与材料相关的常数。

弹道极限速度计算的THOR方程表述为

弹丸穿透靶板后剩余质量计算的THOR方程为

常见材料用于计算剩余速度和剩余质量的THOR方程参数列于表2.1，用于计算弹道极限速度的THOR方程参数列于表2.2。

表2.1　常见材料剩余速度/质量THOR方程参数

表2.2　常见材料弹道极限速度THOR方程参数

基于冲塞理论的弹道极限方程有所不同。以球形弹丸侵彻靶板过程为例，假设侵彻过程中弹丸无质量损失，并忽略弹丸与靶板摩擦所消耗能量，球形弹丸变形只产生于初始压缩阶段。冲塞过程中，根据能量守恒定律，球形弹丸动能主要转化为塞块和弹丸的剩余动能W1、弹丸墩粗变形消耗的能量W2、惯性压缩作用消耗的能量W3、靶板冲击形成绝热剪切带需要的能量W4。

在初始压缩阶段，假设球形弹丸侵入靶板深度为h1，球形弹丸变形部分处于动态屈服应力状态，墩粗部分可近似为柱体，镦粗变形所需能量为

式中，σp为弹丸动态屈服应力；R为球体墩粗部分半径。

假设球形弹丸初始速度为v1，塞块速度v和弹丸初始速度v1满足关系

惯性压缩阶段作用于弹靶上的作用力主要包括压缩力和剪切力。假设弹丸和靶板作用后共同速度为v2，根据动量守恒定律有

式中，mp、mt分别为弹体和塞块的质量；ρt为靶板材料密度。(www.xing528.com)

惯性压缩作用消耗的能量W3为

弹丸与靶板碰撞后，接触应力为p1，相对速度为0。在接触应力作用下，弹丸产生后退速度V2，则接触面真实速度应表述为

式中，V1为靶板运动速度。

根据动量守恒定律，在撞击时间Δt内，应力波在靶板内传播Δx，则有

由于

弹丸后退速度V2可表述为

弹丸初始速度与接触应力之间的关系可表述为

式中，cp、ct分别为弹丸和靶板中应力波传播速度。

由式（2.19）和式（2.14），可得惯性压缩作用消耗能量为

惯性压缩过程中，弹靶作用区域圆周剪切抗力使弹靶间压力有所增加。此阶段，塞块位移很小，圆周剪切面积近似等于初始剪切时最大面积2πRh2。剪切抗力引起的压应力增量为

式中，τ为材料动态剪切强度；h2为惯性压缩阶段的侵彻靶板深度。当弹丸着靶速度较大时，剪切抗力引起的压应力增量不可忽略，作用在弹靶上的等效压应力为p1＋p2。此时，惯性压缩阶段总消耗能量为

绝热剪切阶段，侵入靶板深度为h3，靶板剪切变形消耗的能量为

由球形弹丸侵彻靶板的三阶段计算模型，可得

式中，v3为球形弹丸和冲塞同时脱离靶板时的速度。

当W1=0时，即弹丸初始速度恰好可穿透靶板，弹道极限速度为v50，则

基于量纲分析法，可在一定假设条件下获得球形弹丸弹道极限速度经验公式。假设球形弹丸为刚体，忽略热效应，认为弹丸飞行弹道为直线，着靶角α仅影响速度方向靶厚，则弹丸对靶板侵彻过程主要受表2.3中参量影响。

表2.3　影响球形弹丸弹道极限速度的主要因素及量纲

弹丸对靶板碰撞过程的物理方程为

式中，Vf为弹丸速度，a、b、c为待定常数。

令

则式（2.27）可表述为

对式（2.28）取对数得到

式中，Y=lnλ1，A=lna，X1=lnλ2，X2=lnλ3。

对式（2.29）中随机函数Y和随机变量X1、X2进行线性回归处理，可获得系数A、b、c。通常，c值变化不大，可取0.3，弹道极限速度表述为

式中，h、ρt、σt分别为靶板厚度、材料密度和强度极限；d、ρp分别为球形弹丸直径和材料密度；a、b为与靶板和弹丸材料有关的经验常数。

典型弹靶材料的a、b值列于表2.4，可以看出，在给定靶板条件下，钨球的a、b值均大于钢球，表明钨球侵彻能力更强，弹道极限速度更低。

表2.4　不同弹靶材料的ɑ、b值