如何处理分析结果数据？

在日常分析中，一般只对每个试样进行有限次的平行测定，那么，若所得的分析数据的极差值不超过该方法对精密度的规定值，均认为有效，可取平均值报出。但对于一些有特殊要求的试样，多次测量的数据是否都那么可靠，都参加平均值的计算，就必须进行合理评价和舍取了。如果在消除了系统误差之后，测得的数据出现显著的大值或小值，这样的数据是值得怀疑的，称这些数据为可疑值。对可疑值应做以下处理：在分析过程中已知数据是可疑的，如试样沾污或溶液溅出，采用燃烧法测碳时试样未燃烧完全，或在复查分析结果时已找到出现可疑值原因，应立即将可疑值弃去，但找不出可疑值原因的，不应随意弃去或保留，而应根据数理统计原则来处理。下面介绍三种检查方法进行判断，以决定取舍。

1.4d法

4d法即4倍于平均偏差法。具体做法如下：

1）除可疑值外，将其余数据求算术平均值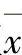及平均偏差。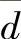

2）将可疑值与平均值相减，若可疑值与平均值之差大于或等于4，则应将可疑值舍去；若可疑值与平均值之差小于4，则应保留可疑值。

例7 测得一组不锈钢中铬的质量分数分别为17.18%、17.56%、17.23%、17.35%、17.32%，问其中最大值17.56%是否应该舍去？

解

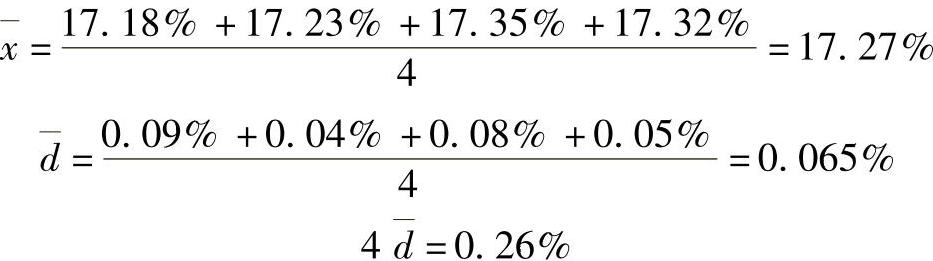
因为17.56%-17.27%=0.29%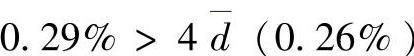，，故17.56%应该舍去。

此方法计算比较简单，适用于4～6个平行数据的取舍。

2.格鲁布斯（Grubbs）检验法

其步骤如下：

1）将所有测量结果的数据按大小顺序排列：

x₁＜x₂＜x₃＜…＜x_n

其中x₁或x_n可能是可疑值，需要首先进行判断，决定其取舍。

2）用格鲁布斯检验法判断可疑值时，首先计算出该组数据的平均值及标准偏差s，再根据统计量G进行判断。统计量G与可疑值、平均值x及标准偏差s有关。

设x₁是可疑值，则

设x_n是可疑值，则

如果G值很大，则说明可疑值与平均值相差很大，有可能要舍去。G值要多大才能确定该可疑值应舍弃？这就要看对置信度的要求如何。表6-3是临界G_α，n表。如果G≥G_α，n，则可疑值应舍去，否则应保留。α为显著性水平，n为测量次数。

表6-3 临界G_α，n表(www.xing528.com)

格鲁布斯（Grubbs）检验法最大的优点是判断可疑值的过程中，将正态分布中的两个最重要的样本参数平均值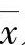及标准偏差s引入进来，故此方法的准确性较好。但相对而言，计算平均值及标准偏差s比较麻烦。

3.Q检验法

其步骤如下：

1）将所有测量结果的数据按大小顺序排列：

x₁＜x₂＜x₃＜…＜x_n

其中x₁或x_n为可疑数据。

2）按式（6-15）计算Q值。

式中 x？——可疑值；

x——与x？相邻的值；

x_max——最大值；

x_min——最小值。

3）查表6-4，比较由n次测得的Q值，与表6-4中所列的相同测量次数的Q_0.90相比较。Q_0.90表示90%的置信度；若Q＞Q_0.90，则相应的x？应舍去，若Q＜Q_0.90，则相应的x？应保留。

表6-4 置信水平的Q值

采用Q检验法时应注意以下几点：

1）适用于测定次数在3～10之间的检验。

2）原则上只适用于检验一个可疑值。

3）若测量次数仅3次，则检出可疑值后勿轻易舍去，最好补测1个或2个数据后再做检验，以决定取舍。