精密度与偏差分析：测量结果的可靠性

精密度是指在相同条件下，多次重复测定的结果彼此相接近的程度，用偏差来度量。偏差也可分为绝对偏差和相对偏差。

绝对偏差=单次测定值-测定平均值 （6-4）

绝对偏差和相对偏差代表单次测定值对平均值的偏离程度，在通常的分析测试工作中用平均偏差和相对平均偏差表示。

例如，对同一试样进行了n次测定，测得的结果分别为x₁，x₂，x₃，…x_n，则其测得的平均值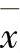（）和平均偏差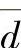（）可分别用式（6-6）和（6-7）计算。

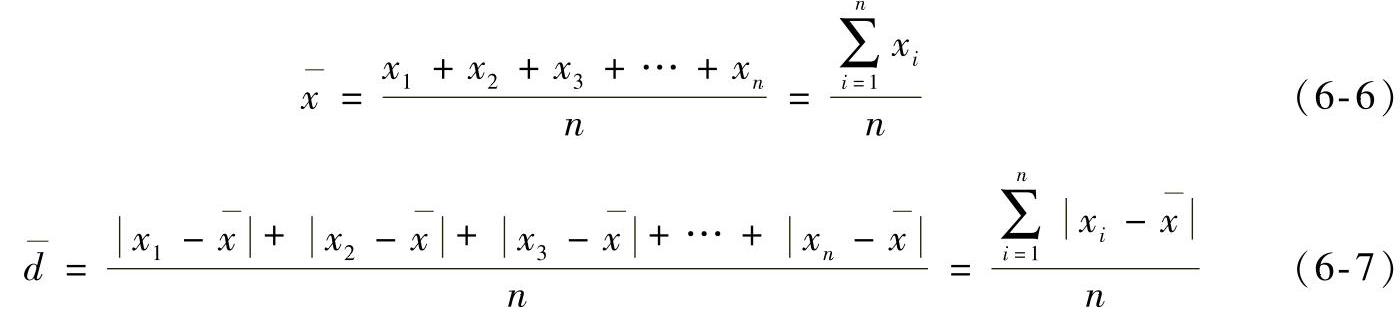
相对平均偏差是平均偏差在测得平均值中所占的百分数，用d_x表示。

用平均偏差表示精密度，方法虽简单，但当测定所得数据的分散程度较大时，平均偏差不能看出精密度的好坏。用统计方法处理数据时，广泛采用标准偏差来衡量数据的分散程度。

标准偏差是指样本中个别测定的偏差平方值的总和除以测定次数减1后的开方值，也称为均方根偏差，以s表示。

如果n数较大（n＞50），则分母用n-1或n都无关紧要。

例3 用滴定法测定某耐蚀合金中镍的质量分数时，五个分析结果分别为37.40%、37.20%、37.32%、37.52%、37.34%，试计算平均偏差、相对平均偏差和标准偏差。

解 计算数据见表6-1。

表6-1 计算数据

1）平均偏差(www.xing528.com)

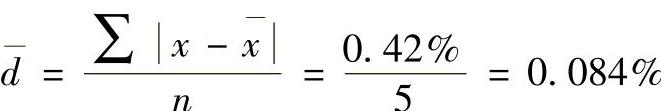
2）相对平均偏差

3）标准偏差

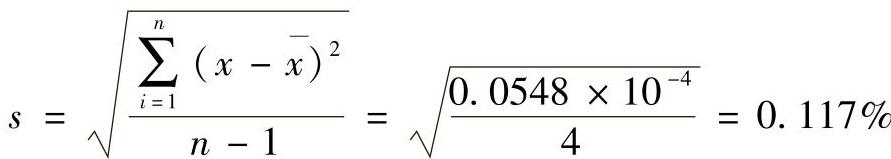
用标准偏差表示分析结果的精密度比用平均偏差更好一些，因为单次测量值的偏差平方之后，较大的偏差就能显著地反映出来，能更好地说明数据的精密度。

有时为了更好地说明分析结果的好坏，也有用相对标准偏差（RSD）或变异系数（VC）来表示精密度的。相对标准偏差代表单次测定标准偏差对测定平均值的相对值，也用百分数表示，其表达式为

另外，对少量数据的评价也用极差来表示。极差又称为全距或范围误差，是测量数据中的最大值与最小值之差，说明数据的延伸情况。对于重复测量次数较少的数据（15次以内），可通过式（6-11）估量标准偏差。

式中 s——标准偏差；

R——极差；

C——与测量次数有关的统计因子，可从相关表中查得。

实际上C值大致地等于测量次数N的平方根，故按式（6-12）也可粗略地求得标准偏差。