优化使用惩罚函数处理等式约束问题

1.惩罚函数的基本思想

前面已经说利用Kwhn-Tacker定理，可以将有约束的非线性规划问题化为无约束的非线性规划问题。而惩罚函数法是一种近似的，但却很有用的求解非线性规划问题的数值解法。其实质是将有约束的非线性规划问题通过选择惩罚因子，变成一系列求惩罚函数的极小值，从而将原始问题转化为求解一系列无约束的极值问题。

惩罚函数的基本思想是建立一个新的目标函数

这个新的目标函数称为惩罚函数，其由两部分组成：

第一部分是原目标函数f（x）。

第二部分为与约束条件有关的惩罚项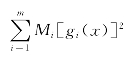，其中Mi是对不同约束方程所加的权，称为惩罚因子，它是一个很大的正数。

从惩罚项可以看出：当约束条件不满足时，因为[gi（x）]2为正值，所以Mi取值越大，则目标函数P（x，Mk）就越大，因此，当约束不满足时，Mi[gi，（x）]2将是一种惩罚；相反，当满足约束条件时，[gi，（x）]2=0，这时不管Mi取多大，P（x，Mk）均与f（x）取相同值，这就是说当满足约束条件时不受惩罚。由此可以看出惩罚因子和惩罚函数的意义。

2.惩罚函数的目的

惩罚函数的目的是建立一个无约束的规划问题，即求惩罚函数P（x，Mk）的无约束极值，意指

其等价于原函数f（x）在等式约束gi（x）=0条件下的最优化问题。

3.惩罚函数的求解方法

设目标函数为f（x），在不等式约束gi（x）≥0（i=1，2，…，m）条件下求极小。

其求解方法可以采用所谓外点法。(www.xing528.com)

（1）外点法用作变换的惩罚函数为

这里，将各约束的加权值Mi取成相同的Mk，而对Mk取

0＜M1＜M2＜…＜Mk＜Mk+1＜…

且

（2）惩罚项中有

（3）解题步骤为：

1）取M1＞0，如取M1=1，给定误差ε＞0，令计算次数k=1。

2）求下式

的最优解X*。

3）检验-gi（x*）≤ε判别式是否满足，若满足，则得到条件极值的最优解xmin=x*，否则，取Mk+1＞Mk，例如Mk+1=αMk，α值可取4或5，令k=k+1，转至步骤2）。

（4）算法的程序流程图如图221所示。

图22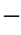1　惩罚函数外点法解算流程