非线性规划的基本问题

在网络补偿中所遇到的问题是在满足一定条件下，来寻求最优的补偿容量和最佳补偿位置。寻优的目的是多种多样的，其可以是补偿后所获得的经济效益最大，也可以是网络损耗最小，还可以是所花费的投资最小，这些要求就构成了规划问题的目标。按照目标的要求，根据规划问题的物理情况，可建立其数学模型

式中　f（x）——目标函数；

max，min——极大、极小值。

正如前面所叙述的，规划问题所追求的目标都是有条件的。例如，要满足系统的功率条件，要满足节点的电压条件，要满足企业的资金条件等，这些条件就构成了问题的约束。约束可以是等式约束，也可以是不等式约束，其可以写成

其中S.T的意义为约束条件；gi（x）=0为等式约束；hj（x）≥0为不等式约束。

式（22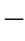1）和式（222）联合起来就构成了非线性规划的基本问题，即追求满足一定约束条件下的最优目标。

例如　(www.xing528.com)

S.T　4x1+5x2≤1500

5x1+3x2≤1575

x1+2x2≤420

xj≥0，j=1，2

便是一个非线性规划问题。所谓非线性是指不论是目标函数还是约束条件，只要有一个是非线性函数，则问题便是非线性规划问题。在所论情况下，目标函数f（x）是x的二次函数，因此，该问题是非线性规划问题。该问题只有5个不等式约束，而没有等式约束。后两个约束条件为x1≥0、x2≥0，因为实际问题往往如此，如x1代表补偿容量、x2代表补偿位置，如果其小于0是没有实际意义的。