纺织企业常用方法优化质量控制

图形表示法是质量控制很常用的表示法，它具有更直观、一目了然的优点。

（一）直方图

直方图又称频率分布图，是整理数据、判断和预测生产过程中质量的一种常用工具。用它来表示产品的质量，可以直观地、全面地掌握某一批产品的质量分布情况。

【例】某粗纱的条干不匀率分组见表7-5。

如图7-14所示，纵坐标表示数据的频数，横坐标表示粗纱的条干不匀率。由于条干不匀率是连续型随机变量，在数轴上的有效范围内是充满的，所以长方块是连续的，其边缘连线就构成了一个阶梯形的图形，称此为直方图。

表7-5　某粗纱条干数据

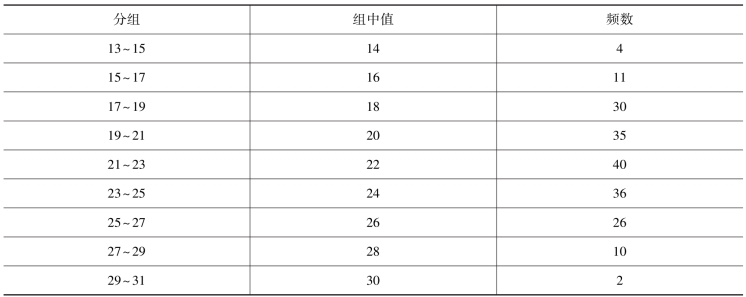
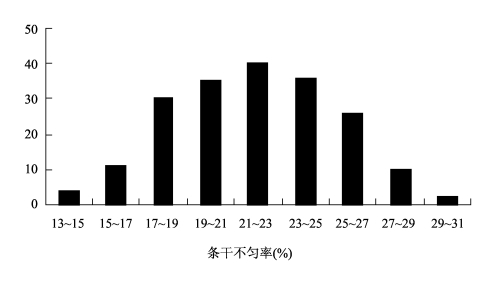
图7-14　某粗纱条干不匀率的直方图

（二）波动图

以横坐标表示时间或数量，纵坐标表示质量指标，所绘出的折线图形，称为产品质量波动图（作图的方法见后面的管理图）。直方图与波动图各有特点，直方图表示试样的集中倾向，波动图是表示波动的平均水平；直方图表示离散趋势，波动图表示质量波动范围。波动图比直方图更能明确地表示出产品质量随着时间而波动的情况，可以及时发现质量问题，以便分析、预测和采取措施加以控制。

（三）因果分析图

因果分析图，又称特征要素图。因其形状犹如鱼刺、树枝，故又称为刺图或树枝图。它是发动和依靠群众寻找影响产品质量的因素，把原因条理化的一种有效方法。其基本格式如图7-15所示。

在运用因果分析图法时，要注意以下几点。

（1）在找原因时，一定要发扬民主，充分听取各方面的意见，一一记录下，决不能简单地搞少数服从多数。

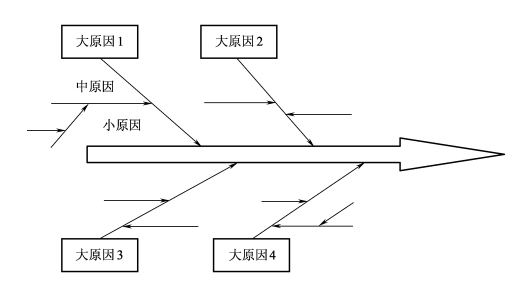
图7-15　因果分析图

（2）原因要分析得细，直到能采取具体措施为止。

（3）要找出原因中的主要原因。尽可能运用数据，做出主次因素分析图（见后）。实在没有或不可能有数据的，也可用民主办法讨论决定。

（4）针对主要原因，采取措施，进入下一个PDCA循环。

【例1】某厂织布车间在解决油疵坯布时，所作的因果图如图7-16所示。

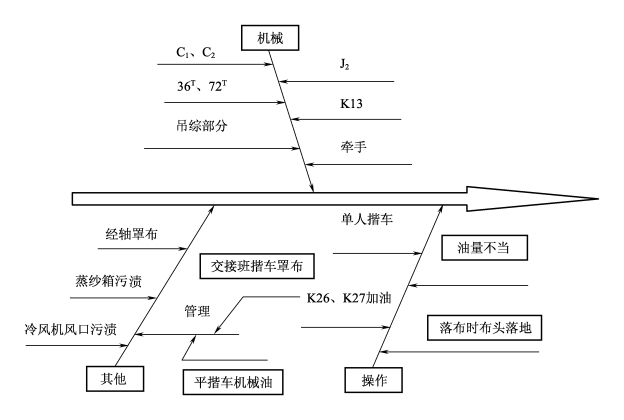
图7-16　织部油疵的因果分析图

（四）主次因素分析图

主次因素分析图，又称排列图（帕累托图）。它也被用于分析生产中的薄弱环节，以找出影响产品质量的主要因素。该图主要是分析因素的主次，按主次排列成直方图和累计曲线，使人看起来清晰易懂，主次分明。

主次因素分析图由两个纵坐标、一个横坐标、若干个直方块和一条曲线组成。左边的纵坐标表示频数（件数、只数等），右边的纵坐标表示频率（以百分率表示）。横坐标表示影响产品质量的各种因素，按因素的大小从左到右排列。曲线表示各因素的累计百分率，此曲线又称为帕累托曲线。

【例2】某厂13.1tex×2×28tex涤棉卡其以分/匹为单位的疵布的主次因素分析如图7-17所示。

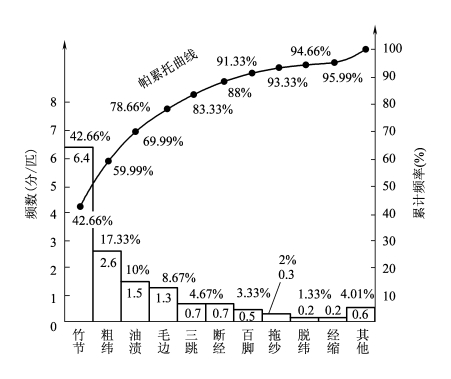
图7-17　13.1tex×2×28tex涤棉卡其以分/匹为单位的疵布的主次因素分析图

【例3】某厂织机经向断头的纺部原因主次因素分析如图7-18所示。

图7-18　织机经向断头的纺部原因主次因素分析图

主次因素分析图习惯上，以累计频率占80%左右的几个因素称为主要因素，其余的称为非主要因素或次要因素。根据主次因素分析图中的主要因素，再进一步分析造成这些因素的原因。如图7-17中竹节的产生原因有纱头搭入、清洁工作不慎而造成的绒板花、挂花、飞花、油花混入等。将这些原因再按主次因素用直方块排列成图，即为分层图，这一方法称为分层法。分层法是一种重要的分析方法。在质量分析中，可以按不同的时间、项目、班别、设备、操作人员等进行分层分析。除了上述主次因素分析图外，分层法还可运用直方图、管理图等形式，其作图方法和它们完全相同，这里不再赘述。

（五）相关图

1.变量间的相互关系　一切客观事物都是互相联系和具有内部规律的。如某一纺织产品质量和它周围的其他事物互相联系着和互相影响着。这种事物之间的相互联系和相互影响，反映到数学概念上，就是变量与变量之间的函数关系。在生产和科学实验中，经常遇到一些变量共处于一个统一体中，它们相互联系，相互制约，在一定的条件下又相互转化。这种变量间的关系分为两类。

（1）确定性关系。这就是常见的函数关系。如纱线的线密度与它的重量、长度之间有一个完全确定的关系，即：

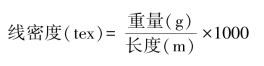
线密度、重量、长度是三个变量，若在这三个变量中有两个已知，另一个就可以精确地求出，它们之间的这种关系就叫作确定性关系。

（2）相关关系。如生条的棉结杂质数与布面的棉结杂质数之间有一定的关系，当生条的棉结杂质数多时，可以知道布面的棉结杂质数将会增加。但是，根据生条的棉结杂质数精确地计算出布面的棉结杂质数是不可能。因为在从生条到织物的整个纺织加工过程中，影响棉结杂质的因素很多，相互之间构成一个很复杂的关系。像这样一种关系在纺织生产中是大量存在的，如纤维的强力与伸长之间；纱的回潮率与原棉含水量之间；纱线强力与捻度之间的关系等。这些变量之间既存在着密切的联系，又不能由一个（或几个）变量的数值精确地求出另一个变量的值，我们称这类变量之间的关系为相关关系。

由上可知，变量之间的确定性关系与相关关系是两类不同的关系，但是应当指出，这两类关系之间并没有一道不可逾越的鸿沟。由于测量误差等多种原因的影响，确定性关系往往会通过相关关系表现出来；当对事物的内部规律了解得更加深刻的时候，相关关系的又可能转化为确定性关系。回归分析就是研究相关关系的一种非常有用的数学工具，可以帮助我们正确的找出变量之间的相互关系。

2.相关图与回归方程　相关图又称散点图，是用来表示两个变量之间的关系的坐标图。若已知变量x与y之间存在着某种相关关系，变量y的值在某种程度上是随着变量x值的变化而变化。通过试验，我们可以得到一批关于x、y的对应数据，每一对x、y的变量，在坐标系上都可以找到一个点，即坐标图上的每一个点，都分别表示两个变量的一对数值。如果这两个变量有相关关系，就可以计算出其回归方程。这种方程可能是直线的，也可能是曲线的。由于曲线方程比较复杂，在这里我们仅介绍直线方程的确定方法。

某厂在高产梳棉机上，分别用SD-3A型和SC-3型两种金属针布纺制28tex（21英支）纱，对道夫速度与生条棉结之间的关系进行试验，测得的数据见表7-6，将数据画在坐标图内（图7-19）即可得到一些点。

表7-6　道夫速度与生条棉结关系

从图7-19中看出，这些点大致分布在一条直线附近，可用一条适当的直线来表示x与y之间的关系，设此直线方程为：

y=a+bx

图7-19　相关图

人们称此直线为变量y对x的回归直线，y=a+bx就称为变量y对x的回归方程。式中，b称为回归系数，在数学上叫作斜率；a为常数项，在数学上叫作截距。这种可以用直线方程来大致表示的两个变量间的关系为线性相关关系。

3.计算回归系数的经验公式　对回归系数的计算可运用微积分求极值的方法求得。此外，常用的还有最小二乘法和平均值法两种。这里仅介绍经验公式——平均值法。

（1）先把观测方程分为两组，使每组方程的个数相等。

第一组y1=a+bx1

y2=a+bx2

……

yn=a+bxn

第二组yn+1=a+bxn+1

yn+2=a+bxn+2

……

y2n=a+bx2n

（2）分组相加。

（3）将以上两个方程相减即可解出b。

（4）再求常数a。(www.xing528.com)

则

所以　

4.回归方程的应用　当知道变量x为某一确定值以后，由回归方程y=a+bx，就可以预测另一变量y的相应数值。如有些纺织企业，为了保证布面的棉结杂质指标在合格品范围内，通过回归方程可以计算出细纱和生条上棉结杂质应该控制的水平。因此，回归线性方程在纺织企业中的应用还是相当多的。此外，从相关图可以很直观地判别两个变量之间相关与否和相关的程度。

在应用回归方程时，必须注意两点。

（1）生产条件一定要与计算时的条件基本相同。若生产条件已经发生了变化，那么回归方程也要作相应的变化，即须重新计算。

（2）回归方程应用时是有一定范围（一般为计算时采用的范围）。如果超出了计算时的范围，正确程度就要受到影响。还需注意，当方程计算以后，自变量与因变量不能互逆，即不能由y=a+bx而导出x的值。

（六）质量管理图

1.质量管理图的作用　质量管理图又称质量控制图，它是对生产过程的描述，是生产稳定性的反映。在质量管理的统计工具中，管理图是核心。借助质量管理图可以判别质量的稳定性，评定工艺过程的状态，及时发现产品质量不稳定的苗头，及时分析研究，排除其不稳定的因素，从而预防不合格产品的产生。质量管理图还可以作为质量评定和交货检验的凭证；又是管理工作中的重要技术档案。借助质量管理图还可以验证技术措施与有关规程的执行效果，正确地做出技术决定，总结提高产品质量的经验。

管理图的种类很多。用于计量特性值的有单值控制图（x控制图）、平均数—极差控制图（T—R控制图）、中位数—极差控制图（x—R控制图）。用于计件特性值的有不良控制图（p控制图）、不良数控制图（pn控制图）；用于计点特性值的有缺陷数控制图（C控制图）、单位缺陷控制图（u控制图）等。

管理图一般由一组纵坐标和横坐标、三根水平的控制线所组成（图7-20）。

（1）纵坐标表示尺度线。

（2）横坐标表示日期或产品的批号等。

（3）中心线（平均值）。

（4）控制上限线。

（5）控制下限线。

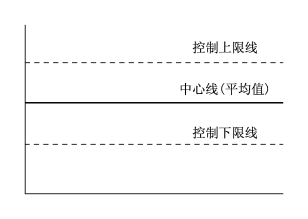
图7-20　管理图

在实际使用中，管理图只有一根控制线的情况也是常有的。如棉结杂质只需要控制上限，那么下控制线就不必要了；品质指标只需要控制下限，上控制线也就不必要了。有的控制线也可以多于两根，可以根据产品质量的具体要求，在控制合格品的区域内，再划分“优良区”“较好区”“警戒区”等，这些均应视具体情况而定。

管理图制成后，将测量结果在图上的相应位置打点。如果这些点落在上限和下限线之间，即落在控制范围之内，原则上可以认为生产过程处于控制状态。点与点之间的差异是偶然差异，这种波动是随机现象，属于正常波动。如果点超出控制界线，即在上限和下限之外，则可认为是失控。出现的差异是系统性差异（即非随机现象），应立即查明原因，采取措施。

2.控制上下限的确定

（1）x±3σ法（亦称千分之三法则）。

此法在机械行业是一种成功的传统方法，但在纺织企业中的应用，不少单位还在摸索之中。在实践中发现对大部分指标的质量控制±3σ范围太宽，故可根据具体情况，采用±2σ或±σ等。

（2）λ±3法。一定长度细纱的疵点，一定面积坯布上的棉结杂质、织疵等空间散布点子，其分布不是正态分布，故确定管理图上的控制上下限，不宜用σ法，而用此法。

式中：C——疵点数；

λ——疵点平均数。

（3）±k%法。按质量的实际要求，规定控制线，必须将质量掌握在此控制线内，且较小为好。此法应用于纱疵率、织疵率、漏验率、坏筒率、棉结杂质等方面。各企业可根据实际情况，总结以往的经验，采用适当的百分率（k%）定出控制界限。

（4）质量标准±公差范围法。按规定的质量标准作为中心线，规定的公差范围作为上下限的控制线，越过公差规定，即属于不合格。在中心线与控制线之间，还可划分优良区、较好区、警戒区、不合格区。如浆纱上浆率、回潮率、断头根数等控制图就属于这种情况。

例如：某厂29.5tex×29.5tex（20英支×20英支）纱卡的上浆率的控制如图7-21所示。

图7-21　29.5tex×29.5tex（20英支×20英支）纱卡上浆率控制图

3.常用的管理图

（1）x—R控制图（图7-22）。这种控制图把平均值（x）和极差（R）两个控制图联系在一起。x图主要用来分析平均值的变化；R图主要用来分析质量波动情况。使用x—R控制图主要是通过此图了解各变量值是否处于被控制状态，即了解各变量值相应地偏离x的R是否属于偶然差异，以便及时掌握其动态。

图7-22　较多的点间断地在同一侧

x和R的控制上限和控制下限的值可以简单地从极差R求得其近似值，从而避免了均方差σ的复杂计算。其计算公式如下：

式中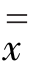：——各批（或各日）平均数的平均数；

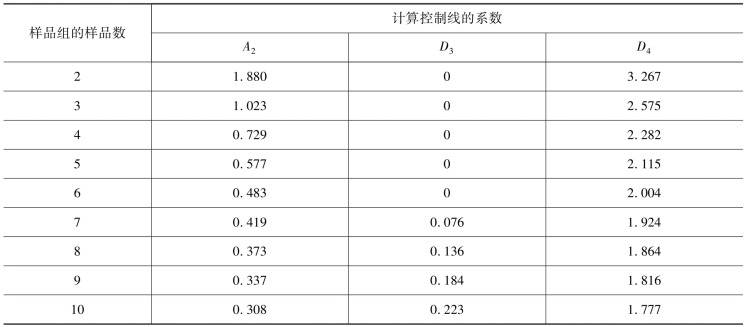
A2、D3和D4各系数可由表7-7查得。

表7-7　x —R控制图用系数

（2）p控制图。p控制图是对产品的不合格品率（p）的控制图。如前所述，在大子样的情况下，不合格品率的分布可视为正态分布，因此仍可用±3σ法则计算出上下限，即：

不合格品率　

平均不合格品率　

（3）pn控制图。也称不合格品数控制图，样本的容量为n，不合格率为p，则不合格品率p乘以样本数n即为不合格品数r，pn控制图就是用于控制r值的。当样本大小相同时，将p控制图转换成pn控制图，可以省去对不合格品率的计算。

（4）C控制图。也称缺陷数控制图，用于控制一定长度、一定面积或任何一定单位中所出现的缺陷数目（C），如布匹疵点数等。

（5）u控制图。也称缺陷率控制图，u表示每单位中包含的缺陷数（即缺陷率）。与C控制图不同的是，u控制图不需要样本长度或面积始终一定，但必须将缺陷数换算成单位缺陷数后，才能使用u控制图。

4.对管理图的观察分析　将测量结果在管理图上的打点，不外乎出现点超出界限或在控制界限之内两个可能。原则上可根据点的出界或不出界来判断生产过程是否处于控制状态。但是，根据数理统计的基本规律，在生产正常的情况下，点出界的可能性为1‰左右，因此，如果有点出界就判断生产异常，可能会犯虚发警报的错误（数学上称为“第一种错误”）。为此，有下列判断准则。

在基本上是随机排列的情况下，连续25点全部落在界限之内，或连续35点出界不超过1点，或连续100点出界不超过2点，即可以判断生产过程仍然处于控制状态，但对点出界的产生原因必须查明。

另一种情况是，生产过程虽然出现了异常，但某些产品质量特性值在控制图上却都处在控制界限之内，这时，如果判断生产过程正常，则会犯漏发警报的错误（数学上称为“第二种错误”）。为此，可采用下列判断准则。

（1）有若干个点连续出现在中心线一侧（称为“连”）。一般有5点相连时，要注意操作方法；有6～7点相连时，要引起警惕；连成的点在7点以上的即可判断为异常。

（2）有较多的点间断地出现在中心线一侧。如连续11点中至少有10点在一侧，14点中至少12点在同一侧，17点中至少有14点在同一侧，20点中至少有16点在同一侧，即可判断为异常（图7-22）。

（3）有若干点连续上升或下降。当连续有不少于7点上升或下降时，属于广义趋向，是一种明显的异常（图7-23）。

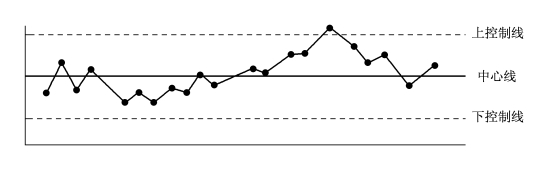
图7-23　广义趋向

（4）有较多点接近控制极限。当点子较多地（如3点中有2点，7点中有3点，10点中有4点等）接近控制极限，即处于控制的边缘状态时，也是一种异常情况。

（5）有若干点周期性变化或集中在中心线附近。有若干个点子出现周期性变化或波浪式的周期性变化的情况，或所有的点子都集中在中心线附近，均属异常。

凡出现上述“异常情况”，一般都有异常的因素潜伏着，必须立即进行调查，究其原因，采取措施，防微杜渐，保证产品质量的稳定良好。这是用好管理图，使之更好地为生产服务的重要环节。