频率分布特征数及其计算方法

（一）离散型随机变量和连续型随机变量

在纺织企业的生产过程中随机现象和随机事件大量存在。通过科学的方法来研究这些事件进而解决问题时经常需要做大量的工作。在纺织企业的生产中，通常会碰到的随机变量有离散型和连续型两种。

1.离散型随机变量　在纺织企业生产过程中，有些随机变量，如生条、纱线上的棉结杂质粒数，细纱、布机上的断头数等，都只能出现0、1、2、3等正整数，在数轴上只能取一个个孤立的值，相互不连续。这类变量我们称为离散型随机变量。

2.连续型随机变量　一类随机变量，如棉纤维的长度、生条的重量、纱的强力、织物的弹性变形量、温度与湿度等，这类变量往往不是整数，在数轴上该变量不再是一个个孤立的点，而是在有意义的范围内，可以充满任何区间。这类变量称为连续型随机变量。

（二）频数和频率

在一批数据中，某一数据出现的次数，称为该数的频数（f）。一批数据的总频数就是这批数据的总数。某一数据出现的频数与总频数的比值，称为频率（f′）。

（三）算术平均数

1.算术平均数是一个特征数　在工业生产中经常用子样的算术平均数来估计其总体的平均水平。总体平均数记作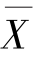 。则其计算方法为：

一批数据为 X1、X2、X3、…、Xn（共有 n 个数据），则：

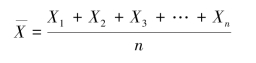
即

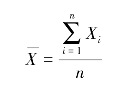
在实际生产中，由于生产量很大，总体平均数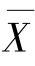是不易得到的，或者根本不可能得到的。总体平均数在数理统计中又称“数学期望”（数学期望是平均值的推广，即“加权”平均值）。因此，在大量子样条件下，可以将子样平均数作为总体平均数的估计值。

2.加权平均数是分组法的算术平均数　如要检测一批原棉纤维的平均长度，通常每次的实际抽样量达上万根纤维。要把它们一根根地测量出来，这在实际工作中是不可能的，也是不现实的。目前一般采用重量加权平均的办法计算。若纤维的根数为n，分组数为k，则加权平均数的计算方法为：

设每组纤维的平均重量为 W1、W2、W3、…、Wk，每组纤维的平均长度为 X1、X2、X3、…、Xk。

则，这批纤维的平均长度为：

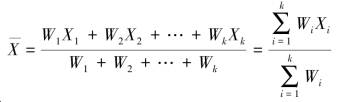
上式可用频数表示为：

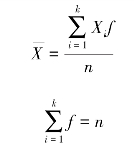
（四）极差和均方差

极差R是表示一批数据中最大数（L）与最小数（S）之差。

R=L-S

极差（R）反映了一批数据的波动情况，这是数据离散程度的一种表示方法，而且计算也很简单。为了更精确地反映一批数据的波动程度（即离散程度），可用均方差这一特征数来表示。

均方差，又称标准离差或标准偏差，或简称标准差。一般总体均方差用σ表示，子样的均方差用s表示。均方差比极差的精度高。均方差的计算公式：

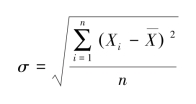
对于频率分布表达的情况为：

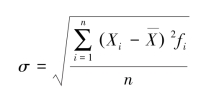
式中：fi——频数。(www.xing528.com)

一般当样本为小子样的时候，即n<50的均方差的公式中的分母取n-1，即：

式中：n-1——自由度。

（五）平均差

平均差是指各测量值与平均数之差的绝对值的平均数，用d来表示，为了计算上的方便，纺织企业常用平均差表示产品质量的离散程度。计算公式如下：

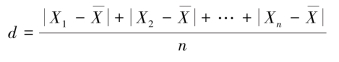
（六）不匀率

1.乍密尔不匀率（H）

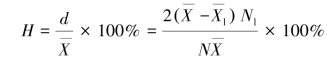
或

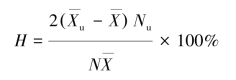
式中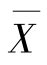：——试样的平均数；

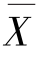u——平均数以上各数的平均数；

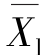1——平均数以下各数的平均数；

N——试样总数；

Nl——平均数以下的数据数；

Nu——平均数以上的数据数。

乍密尔不匀率又称平均差系数，这是纺织厂中常用以反映试样离散性的指标。

2.变异系数CV

CV=A×H

式中：H——平均差系数；

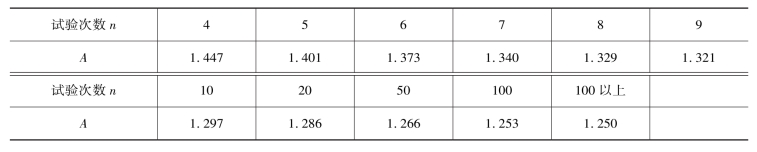
A——系数（表 7-4）。

因为

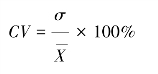
所以　　σ=CV×

表7-4　系数A与试验次数n的关系