碳纳米管增强镁基复合材料应力传递理论分析

把碳纳米管视为短纤维增强相时，根据应力传递理论——剪切滞后分析，可以通过碳纳米管纤维的微元平衡方式来分析沿碳纳米管长度方向应力的分布^[102]，如图3.6所示。

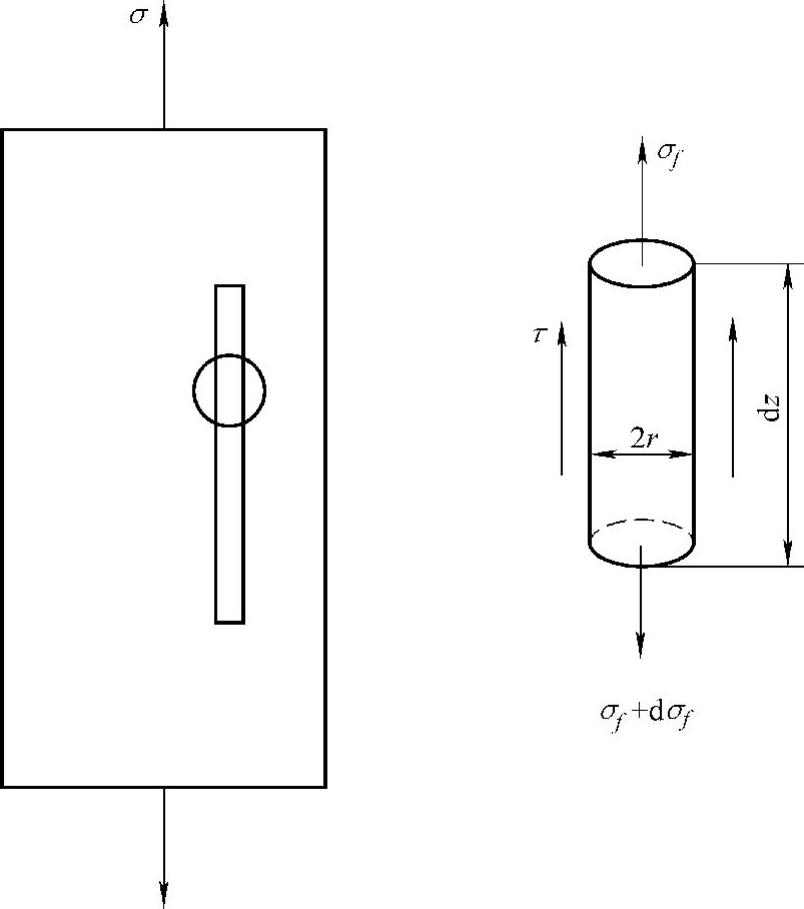
图3.6 碳纳米管长度微元上力的平衡

取碳纳米管长度微元dz，在平衡时要求满足公式（3-1）

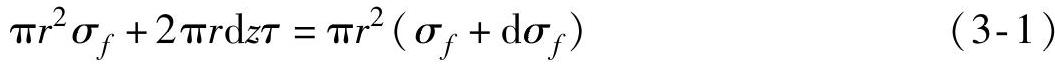
即

式中，σ_f为碳纳米管轴向应力；τ为作用于碳纳米管与基体界面的剪应力；r为碳纳米管半径。

由公式（3-2）可知，碳纳米管增强复合材料中碳纳米管所受应力的增加率与碳纳米管与基体界面的剪切应力τ成正比。对公式（3-2）两边积分得到碳纳米管端部处横截面上的应力σ_f，即

式中，σ_f0为碳纳米管端部应力。

在受力状态下，由于碳纳米管端部高应力集中的原因，与碳纳米管端部相接的基体必将发生屈服或端部与基体分离，因此可以忽略σ_f0这个量。由式（3-3）可知，只要知道了沿碳纳米管长度上界面的剪切应力τ的变化就可以求解出右边的积分值。但这个剪切应力τ是不知道的。为了求出这个解析式，就必须对碳纳米管相邻材料的变形和碳纳米管端部情况作如下假设：与碳纳米管相邻的基体材料是完全塑性的，碳纳米管端部的正应力和碳纳米管中部的界面剪切应力为零。这样，沿着碳纳米管长度的界面剪切应力就是常数，并且等于基体剪切屈服应力σ_y，忽略σ_f0，可得式（3-4）。

对于复合材料中的短纤维，最大应力出现在纤维中部（z=1/2）^[102]，代入则有

式中 l——碳纳米管长度。(www.xing528.com)

碳纳米管的承载能力存在一个极限值，这个极限值就是相应应力作用于连续纤维增强复合材料时的纤维应力。

式中，σ_c为作用于复合材料的外加应力；E_c为复合材料的弹性模量。

把复合材料中纤维载荷传递长度l_f定义为能够达到最大纤维应力（σ_f）_max的最短纤维长度，载荷从基体向纤维的传递就发生在纤维的l_f长度上。

式中，d为纤维直径。

由式（3-7）可知，纤维的载荷传递长度l_f是外加应力σ_c的函数。把与外加应力无关的临界纤维长度定义为l_c，则可以达到纤维允许应力σ_fu（纤维强度）的最大纤维长度为

式中，l_c为临界纤维长度，也就是载荷传递长度的最大值。

图3.7所示为纤维增强复合材料所受外加应力一定时不同纤维长度上纤维应力和纤维/基体界面剪切应力的分布。

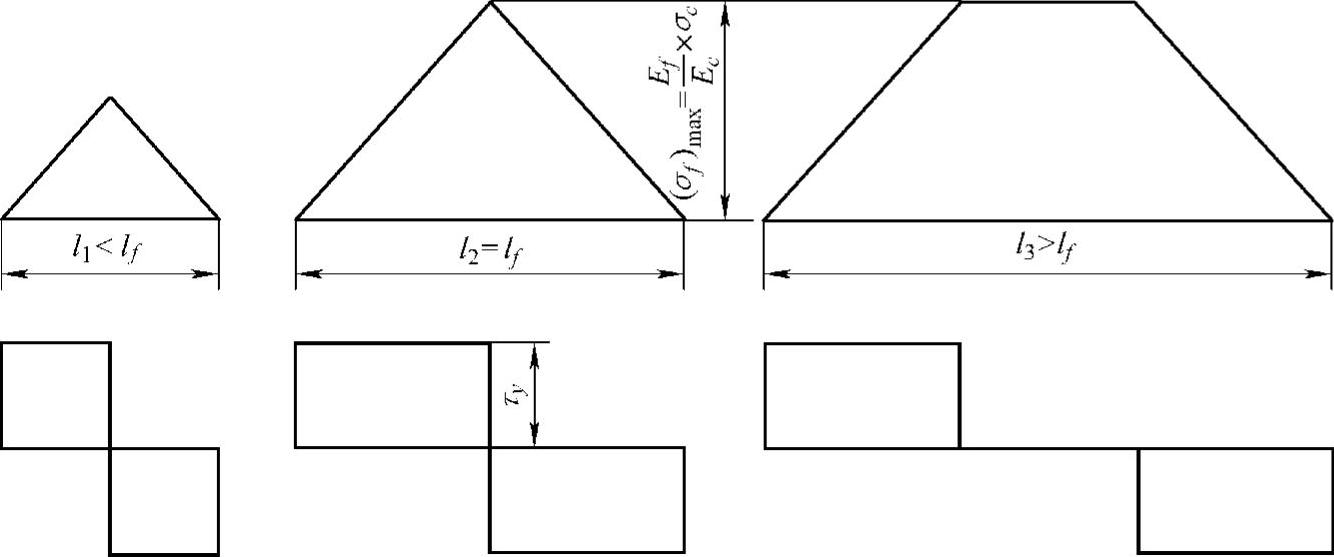
图3.7 纤维应力和界面剪切应力沿纤维长度的分布

由图3.7可以看出，在纤维端部的一定距离内，纤维承载的应力要小于最大纤维应力，这会直接影响复合材料的弹性模量和强度，在纤维长度大于载荷传递长度l_f时，复合材料的行为与连续纤维复合材料相似。