基于非理想界面的类平行板电容器模型优化

为了验证类平行板电容器的非理想界面模型，我们将其运用到rGO/PP纳米界面复合材料中去，并与Wang等[136]的实验结果相比较。其他相关的材料性质在表7.2中给出。下面给出计算结果。

7.5.2.1　由于电子跃迁引起的频率相关MWS效应

第一步，分别阐述MWS效应，加载频率f以及石墨烯和聚合物间导电性的不同Δ 对界面导电性和介电性的影响。计算显示和两者均强烈依赖于f和Δ ，如图7.10(a)和(b)。更重要的是，和均随Δ 的增加而显著提高。这是MWS效应的来源[135]。当Δ 增大时，通过界面的电子数量和积累在界面上的电子数量均增加。此外，界面导电性随AC频率增长而提高，同时界面介电性随之降低。其背后的物理机制可以解释为，当AC频率增加，通过跃迁效应跨过界面的电子数量得到提高，同时界面上积累的电荷数量减少。计算所得界面导电性和介电性将通过有效介质法转换至石墨烯纳米复合材料的有效性质。

图7.10　在三种导电性差异下由于频率相关的Maxwell-Wagner-Sillars效应导致的额外(a)界面导电性和(b)介电性

7.5.2.2　在恒定频率下纳米复合材料关于石墨烯含量c1的相关性

图7.11　在给定频率1000Hz下rGO/PP纳米复合材料有效(a)导电性和(b)介电性关于石墨烯含量的变化

接下来将探究石墨烯纳米复合材料有效导电性和介电性在固定频率下关于石墨烯含量c1的变化。结果通过在固定频率下求解方程(7.6)获得。三种界面条件在图7.11中展示。初始的计算在理想界面条件下进行，如图7.11(a)和(b)中的绿线。两条曲线均比红点标注的实验数据要高。这显示了非理想界面的存在。然后，具有固定 int和κint的计算结果在黄线中表示。由于弱界面效应，可以看到一个明显的下降。然而，这两条曲线均相对平滑，且在达到渗流阈值后比实验数据要低。这表明方程和(7.32)中界面隧道效应以及频率相关的MWS效应的影响需要被考虑。当考虑所有界面效应后，计算结果在蓝线中表示。这两条曲线均在达到渗流阈值后展现出一个显著的提高，并且与实验数据十分接近。这清楚的表明，对于石墨烯复合材料的有效导电性和介电性，静态和动态界面效应都十分重要。

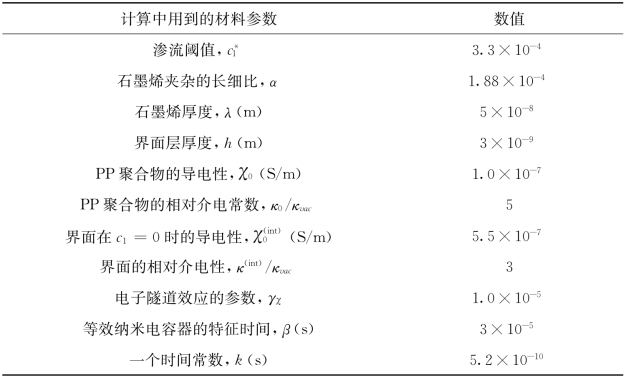
表7.2　计算有效导电性和介电性用到的物理性质，通过Wang等[136]的实验验证(www.xing528.com)

7.5.2.3　石墨烯-聚合物纳米复合材料频率相关的导电性和介电性

最后，研究AC频率和石墨烯含量对纳米复合材料有效导电性和介电性的影响。计算考虑所有界面因素，以及三种不同的石墨烯含量。注意到渗流阈值为＝0.033%。

图7.12(a)和(b)给出了在三种石墨烯含量c1＝0.008%，c1＝0.03%以及c1＝0.08%下，有效导电性和介电性随AC交流频率在范围103 和107 Hz内的变化。图中包含了实验数据以及理论预测。与采用唯象模型的结果类似，在给定c1下有效导电性随AC频率f的增加而增长，有效介电性随频率的增加而下降。这是方程(7.32)中界面效应和的反映。额外的电子会跨过石墨烯-聚合物的界面，导致了一个更高的界面导电性。这三条曲线在低频范围内有十分显著的不同，但在高频范围内趋于融合。可以得出结论，类平行板电容器的非理想边界条件可以很好的抓住石墨烯纳米复合材料频率相关有效导电性和介电性的特征。

图7.12　rGO/PP纳米复合材料在三种石墨烯含量下有效(a)导电性和(b)介电性关于交流频率的变化

7.5.2.4　界面厚度对石墨烯-聚合物纳米复合材料有效导电性和介电性的影响

最后，探究界面厚度对石墨烯-聚合物纳米复合材料有效导电性和介电性的影响。计算在频率为1k Hz并且考虑所有界面因素的条件下进行，结果在图7.13中显示。图7.13(a)指出，由于弱界面层的存在，有效导电性随界面厚度的增加而降低。然而，有效介电性相对于不同的界面厚度几乎保持不变，如图7.13(b)所示。影响有效介电性的主要因素为MWS效应而不是弱界面。

图7.13　rGO/PP纳米复合材料在三种界面厚度下有效(a)导电性和(b)介电性关于石墨烯含量的变化