类平行板电容器非理想界面的模型分析

本小节将讨论基于类平行板电容器的非理想界面。界面的电子隧道效应同7.4.1小节中方程。对于MWS极化，我们将从类比平行板电容器的角度研究其对频率相关的界面导电性和介电性的影响。

由于电荷不能够自由的跨过界面，石墨烯和聚合物间导电性巨大的差距(即1 ≫0)将导致界面处大量电荷的积累。因此，可以将界面比作一个纳米电容器，其上积累的电荷与界面导电性差异(1－0)直接成正比例。MWS效应的产生机理可以解释为石墨烯-聚合物界面处形成的许多纳米电容器。为了研究它对频率相关界面效应的影响，我们采用RC电路表示界面所受到的AC交流电场。

如图7.5所示，每一处界面(绿色区域)可以用在石墨烯相(蓝色区域)和聚合物相(黄色区域)之间的纳米电容器代替。纳米电容器可以看做是由平行板电容器(C)和阻抗(R)串联组成。其中，平行板电容器代表了界面对电荷的积累效应，阻抗代表了界面对电流的抵抗效应。当加载AC交流电场时，电荷会跨过纳米电容器，使界面导电性增加，但同时使界面处积累的电荷减少。因此，这额外增加界面层导电性同时减少界面层介电性。为了简化分析并让模型更具通用性，可以将这些纳米电容器等价为一个等效的纳米电容器，如图7.2所示[135]。

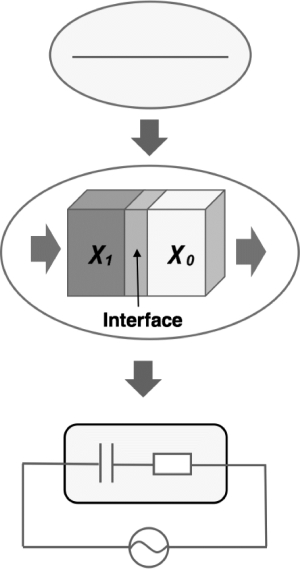
图7.5　由于石墨烯与聚合物基质间导电性巨大的差异所导致形成的纳米电容器原理图

为了推导纳米电容器频率相关的电学性质，我们给其施加一个整体交流电压

其中，为电压的大小。对应的电场强度为

在等效RC电流中，电容器上的电压VC(t)可以用以下微分方程表示

其中，R和C 分别为纳米电容器的电阻和电容，h是界面厚度。方程(7.26)的稳态解为

其中，，以及β＝RC 是纳米电容器的特征时间。

积累在纳米电容器上的电荷Q 直接正比例于导电性的差异(1－0≡Δ )。因此我们有Q＝QC～Δ 。同时，电容器上的电荷QC也和其电压VC关于电容C成比例，即(www.xing528.com)

其中，k为时间单位的系数，A 为界面处横截面面积。因此，等效RC 电路中由于频率相关的MWS 效应而产生的电流为

对应的电流密度为

最后，由于MWS效应产生的复导电性可以定义为

它可以通过方程(7.30)得到，。通过其实部和虚部给出了由于MWS效应引起的界面导电性和介电性

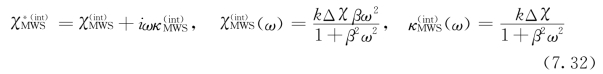
方程(7.32)表明，当AC频率增加，界面导电性增加但界面介电性下降。二者都强烈依赖于石墨烯和聚合物间导电性的不同(Δ )。ω和Δ 对于控制MWS效应均有重要影响。此外，当ω→0时，可以退化为电容器的电容；当ω→∞时，可退化为阻抗的导电性。在本模型中，和随AC频率的变化可统一解释为电子跃迁过程。

结合方程和方程(7.32)，界面层的导电性和介电性针对电子隧道效应和频率相关的MWS效应进行修改

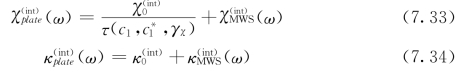
其中，和代表了界面层最终的导电性和介电性，取代方程(7.13)～(7.14)中原始的和以计算包含非理想界面石墨烯夹杂的导电性和介电性。计算得到的和代入方程(7.6)中，计算整体复合材料频率相关和组份相关的有效导电性和介电性。

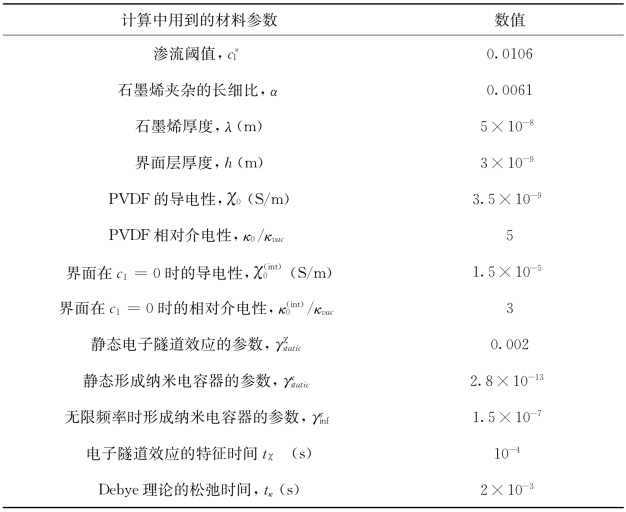
表7.1　计算有效导电性和介电性用到的物理性质，通过He等[132]的实验验证