唯象视角下的非理想界面模型优化方案

本小节将讨论唯象的非理想界面。界面层的导电性和介电性，和，不能随着石墨烯体积分数的增加而保持恒定。随着石墨烯体积分数增加，各个填充物间的距离持续减少，这增加了界面上电子隧道效应和形成微电容器的概率。在石墨烯含量达到渗流阈值后，相连的石墨烯网络开始建立，这一改变更加明显。将石墨烯相连网络的形成看做是一个统计过程，Wang等[123，124]建议采用Cauchy统计函数，，来描述界面隧道效应的影响。这一函数依赖于石墨烯的体积分数c1，在低c1时的值很低，当c1超过渗流阈值时它的值得到极大增加。石墨烯含量的增加同时也提高了石墨烯-聚合物界面上形成微电容器的概率。根据MWS理论，相邻两相材料导电性的不同将在界面上产生极化并积累电荷[28，135，275]。由此导致了界面处许多微电容器的形成，如图7.2所示。为了描述这一现象，Hashemi和Weng[152]证明了Cauchy统计函数也可用于描述界面层介电性的增长[152]。因此，界面层的和都需要修改来反映其c1相关性。

为了表示上述界面现象，基于Cauchy积累密度函数，引入一个通用的抵抗函数

其中

图7.2　由于交流电场下大量纳米电容器的形成导致的Maxwell-Wanger-Sillars效应原理图

γ是一个标量参数，表示在渗流阈值附近的增长幅度。F和τ的c1相关性在图7.3(a)和(b)中表示。它体现了在渗流阈值附近急剧增加，同时对应降低。在这些界面效应作用下，界面导电性和介电性从和修改为

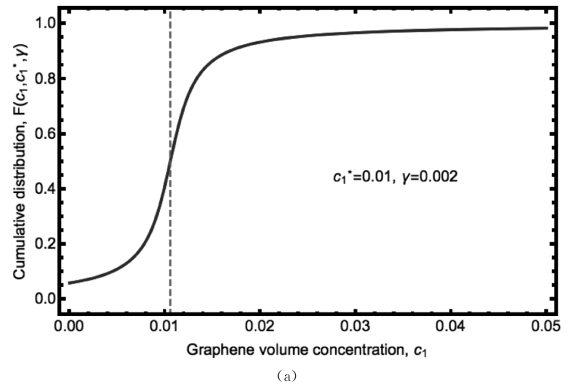
图7.3　(a)Cauchy累计分布函数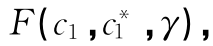，显示了渗流阈值附近增加的界面隧道效应，(b)抵抗函数，显示了渗流阈值附近急剧下降的变化

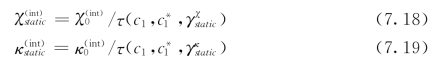
其中，下标“static”表示这些改变是频率无关的，和为相应的标量参数。这一对新的量，和，将代替原来方程(7.13)和(7.14)中的和，以提供被包裹的石墨烯含有静态界面效应的和。(www.xing528.com)

除去静态界面效应，加载频率对界面层的导电性和介电性也有重要影响。只有当这些效应都被考虑后才能得到AC交流载荷下完整的界面效应。注意到界面电子隧道效应在交流载荷下是一个频率相关的现象。在AC频率下，额外的电子从一个石墨烯夹杂跃迁到另一个上。Dyre[140]建议采用一个跃迁函数，p(ω)，来描述这一额外的影响。界面层的静态导电性在加载角频率ω 下增长到动态情形

其中，p(ω)是Dyre跃迁函数

t 是电子隧道效应的特征时间，ω对的影响可以在图7.4(a)中显示。这种效应在高频范围内效果极强。

图7.4　由于AC交流载荷额外的界面效应关于频率的变化：(a)界面导电性和(b)界面介电性

相反，界面层的介电性随频率的增长而下降。它的效果和AC频率下绝缘体的表现很相似。由于AC频率下额外的电子跃迁效应，积累在石墨烯界面上的电子数量减少。这使得MWS极化效应减少，界面介电性降低。根据Debye介电松弛理论[127，141]，在角频率为ω 时增大至

其中，tκ是指松弛时间，是指界面层在无限频率时的介电常数

是无穷大频率下纳米电容器的标量参数。随频率的变化见图7.4(b)。在高石墨烯含量下由低频至高频变化过程中有明显的下降；但在低石墨烯含量下关于加载频率没有明显可见的变化。

至此，唯象的非理想界面模型得到完整的建立。方程(7.20)和(7.22)中和代表了唯象非理想界面模型中界面层最终的导电性和介电性。它们将分别取代了方程(7.13)和(7.14)中原来的和，从而给出了石墨烯相最终的复导电性，*i＝ i＋iωκi。它将被用在方程(7.6)中计算石墨烯纳米复合材料最终的有效复导电性*e 。通过*e ＝ e＋iωκe，纳米复合材料有效导电性和介电性可以分别通过复导电性的实部和虚部获得。