rGO/Cu纳米复合材料的塑性、渐进损伤与破坏分析

现在，调查石墨烯含量对纳米复合材料的塑性、渐进损伤和破坏的影响，并和实验数据进行对比。根据实验参数，三种石墨烯含量分别取为c1＝0，1%和2.5%。第一种对应于基质材料，后面两种对应于rGO/Cu纳米复合材料。

图6.7显示了这三种石墨烯含量下的应力-应变曲线。每一种情形的初始线性部分对应于上述讨论的弹性阶段。在屈服点之后，由于延展性金属基质的硬化作用，真实应力非线性增长。增长率由于渐进损伤的开始而逐渐减慢。曲线到达最大值标志着纳米复合材料的最大强度。后来，由于金属相渐进损伤的作用逐渐增大，真实应力开始降低。最终，真实应力快速降低至0，标志着纳米复合材料的破坏。对应的实验数据也包含在其中。整体上，理论预测与实验结果相一致。特别注意到，当石墨烯含量从0增长至1%再增长至2.5%时，最大强度稳定增长，破坏应变急剧降低。但同时也观察到在应力-应变曲线的最后阶段理论预测与实验值产生不同：理论预测值突然下降，然而实验值平缓变化。最终阶段的破坏过程是由快速的孔洞扩展过程所控制，不能由本理论模型描述。

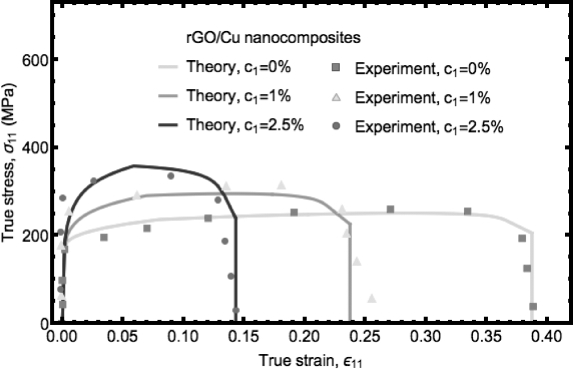
图6.7　rGO/Cu纳米复合材料不同石墨烯含量下应力-应变曲线理论预测和实验值的比较

石墨烯纳米复合材料强度与延展性关于真实应变相反的变化趋势可以通过损伤变量D 的演化来解释，如图6.8所示。损伤变量在达到σ(0)e＝σcr之前保持为0。这表明在整个弹性阶段和初始塑性阶段，没有损伤现象发生。在越过门槛值之后，损伤变量D 开始从0最终增长至1。在高石墨烯含量为c1＝2.5%时损伤变量的增长非常快。越陡的增长导致纳米复合材料更早的破坏。对应的孔洞扩展由图6.8中的虚线所示。破坏时的最大孔隙率在c1＝2.5%时达到0.26，在c1＝1%和0时分别为0.24和0.22。破坏发生在最大孔隙率处，如图6.7中的垂直线所示。同时可以看出，损伤变量在高石墨烯含量时更早的开始增长。这是由更高的等效应力σ(0)e引起的，如图6.9所示。结合图6.8和6.9

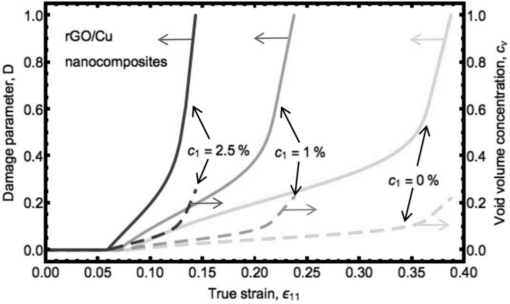
图6.8　rGO/Cu纳米复合材料不同石墨烯含量下损伤变量和孔隙率关于真实应变的变化

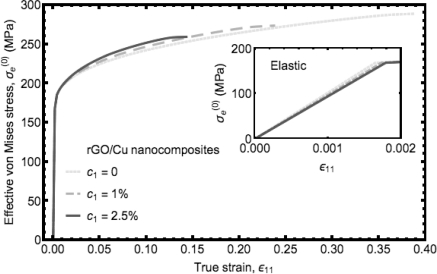
图6.9　rGO/Cu纳米复合材料不同石墨烯含量下损伤基质中有效Mises应力关于真实应变的变化(www.xing528.com)

可以发现，在拉伸应变为0.05时，尽管延展性金属已经进入塑性状态，仍然没有损伤过程发生。所以在早期塑性变形阶段，没有渐进破坏过程。此外，石墨烯含量对塑性变形的开始也有影响，更高的石墨烯含量中会导致金属相弹性阶段更低的等效应力。这会推迟塑性变形的开始，如图6.9中的插图所示。

图6.10展现了rGO/Cu纳米复合材料的损伤速率作为拉伸应变的函数。该变化率在达到之前保持为0。在一个跳跃增长后，损伤速率在一段变形范围内小幅下降。这个小幅下降或者几乎不变的过程是图6.8中损伤变量线性增长的来源。在这一阶段后，变化率急剧上升，这使得损伤变量在最后阶段急剧增长，并最终导致了图6.7中应力-应变曲线最终走向破坏。特别对于高石墨烯含量下的高损伤变化率，损伤变量迅速增长至1。这是图6.7中石墨烯含量为c1＝2.5%情况下纳米复合材料低破坏应变的原因。

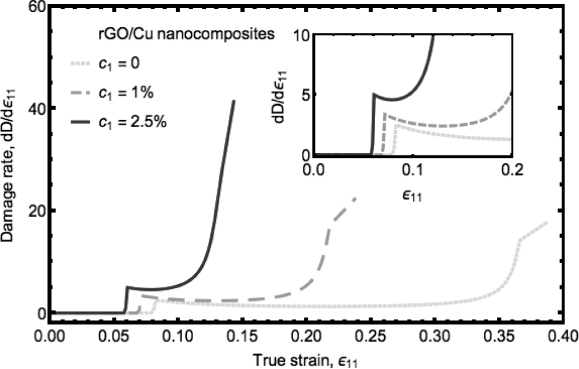
图6.10　rGO/Cu纳米复合材料不同石墨烯含量下损伤变的变化率关于真实应变的变化

同时，我们也将本多尺度理论应用于理想和非理想界面条件下，计算纳米复合材料最大强度和破坏应变关于石墨烯含量连续变化的过程。拉伸强度和破坏应变的结果分别在图6.11(a)和(b)中显示。随着石墨烯含量c1的增加，拉伸强度单调增加，破坏应变急剧减小。整体的计算结果与实验结果相匹配。当石墨烯含量从0增长至2.5%，拉伸强度从250MPa增长至350MPa，达到40%的增长幅度。另一方面，破坏应变从0.39减少至0.14，达到64%的减少幅度。对比图6.11(a)和(b)中理想和非理想界面条件的计算结果，非理想界面对拉伸强度的影响可以忽略，并且对破坏应变的影响也十分小。Hwang等[119]实验中表明石墨烯和Cu基质间具有十分强的粘附能，故这是合理的。他们测量的粘附能达到164J/m2，比在Cu基质上生长出石墨烯的粘附能0.72J/m2要高许多。这一结论与图6.5(a)和(b)中的结果一致。在石墨烯含量在c1＝0.025范围内，理想和非理想界面的有效弹性模量的区别仅为5%。但如果非理想界面指数ρ0继续增大以获得一个更弱的界面，拉伸强度会明显减小并且破坏应变会显著增大，如图6.12(a)和(b)。此时，理想和非理想界面的区别会变得明显。

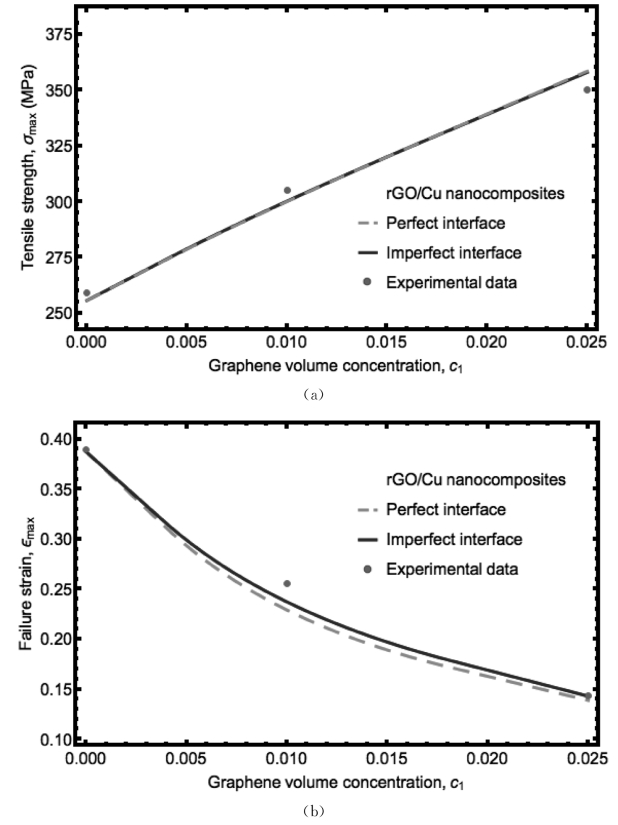
图6.11　rGO/Cu纳米复合材料在理想和非理想界面条件下(a)拉伸强度和(b)破坏应变关于石墨烯含量的变化

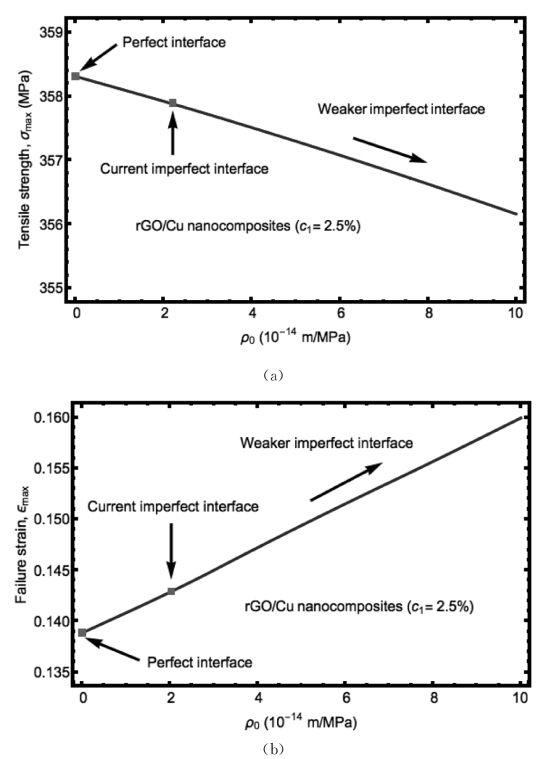
图6.12　rGO/Cu纳米复合材料在c1＝2.5%下(a)拉伸强度和(b)破坏应变关于非理想界面参数的变化