铁电双材料的优化研究

在本节中，我们将向量积分运用于铁电双材料不同裂纹面电边界下。铁电双材料(标注为材料Ⅰ和材料Ⅱ)分别占据着上下两个半空间。考虑一个有限长度的二维裂纹位于铁电双材料界面处，如图5.2所示。这里引入一个面内坐标系系统：x1轴平行于裂纹，x2轴垂直于裂纹，并且原点固定在界面裂纹右端点。

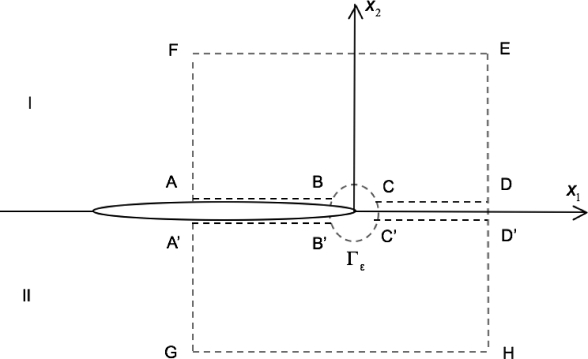
图5.2　铁电双材料有限长度界面裂纹闭合积分路径

除去相场序参数的控制方程，其在接触面和裂纹面的边界条件也应该相应给出。考虑相场参数沿接触表面保持连续

其中，上标“＋”和“－”分别表示上下界面。然后，可以得到接触面处的守恒积分关系

至于裂纹表面，无拉力的边界条件仍然有效，力边界条件和微力边界条件可分别设为无外力和无微力

考虑到铁电单晶体的特点，我们集中讨论电导通，电绝缘，以及广义电绝缘这三种电边界条件：

(1)导通电边界条件[78]

假设电势和法向电位移在裂纹面处连续。

(2)绝缘电边界条件[79](www.xing528.com)

假设裂纹面上没有电荷。

(3)广义绝缘电边界条件[113]

假设裂纹面上存在电荷密度为ω0的恒定电荷层来平衡初始极化强度的法向分量。由于绝缘电边界条件在具有初始极化强度的单晶材料中是无效的，广义的绝缘电边界条件由Li和Landis[113]通过修改绝缘电边界条件而提出。

积分曲线CBAFEDC和C′B′A′GHD′C′在每个组份中不含有奇点，因此

叠加方程(5.37)和(5.38)，我们得到

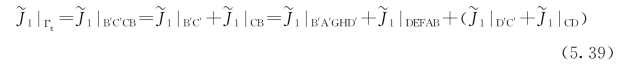
其中，Γε是围绕裂纹尖端的无限小路径。

将界面边界条件方程(5.31)，和裂纹面边界条件方程(5.33)～(5.36)，带入方程(5.39)中，可以得到铁电材料三种电边界条件下的路径无关积分

注意到方程(5.40)将Li和Landis[113]中对于均匀材料的结论推广到铁电双材料中。