这一小节将通过数值计算展示断裂控制参数和电磁屈服区长度随裂纹扩展速度和边界条件种类的变化规律。磁电弹复合材料的每一个组份由BaTiO3作为夹杂,CoFe2O4作为基质混合获得,材料参数在表4.2中给出。BaTiO3和CoFe2O4的极化方向沿着负x3轴。一般意义上,压磁系数确实和所施加的直流磁场有关。由于本研究中磁场加载很小,压磁系数可以简化为常数。
均匀化方法对于磁电弹复合材料是一个很重要的问题。精确的均匀化方法可以参考Bravo-Castillero等[220]关于层状磁电弹复合材料的研究,以及Huang和Kuo[221],Huang等[215],Huang等[222]关于颗粒磁电弹复合材料的研究。目前的研究主要关注裂纹面内电磁场的影响。因此,我们采用一种线性混合的方式[218,223]。磁电弹组份的材料系数可以给为
![]()
其中,λ(i)代表每个磁电弹组份的材料性质,f(i)是压电夹杂在该项组份中的体积分数。为了方便讨论,应力强度因子和局部能量释放率的无量纲参数分别被定义为
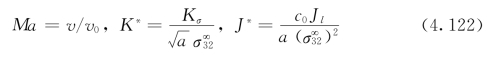
其中,c0=1.0GPa为弹性常数。v0是磁电弹双材料的最小剪切波速
![]()
两种边界条件的计算结果将分别给出。对于材料I和II分别是fI=0.75和fII=0.10。外加力载荷是σ0=-100 MPa。此外,磁电弹复合材料的电磁屈服极限分别给为
![]()
为了保证数值计算的正确性,首先验证裂纹面上的电位移和磁感应强度是否保持恒定。通过设定电磁载荷分别为D0/Ds=0.4和B0/Bs=0.2,计算得到裂纹面内的电位移和磁感应强度,如图4.12(a)和(b)所示,插图表示对应的变化率。可以发现,除了靠近裂纹尖端一小段距离外,Dc(x1)和Bc(x1)在裂纹面内保持恒定。裂尖附近的电磁场由于应力奇异性而增加。对于裂纹面内电磁场,最大的变化率分别为6% 和0.3%。由此验证了4.3.2小节中的假设。

图4.12 当受到力电耦合载荷D0/Ds=0.2以及B0/Bs=0.2时沿裂纹表面(a)电位移和(b)磁感应强度的分布(插图表示对应的变化率)
然后,讨论在不同电磁载荷下裂纹内电磁场随扩展速度的变化趋势。当电载荷增加时,裂纹面内的电位移增加,对应的磁感应强度几乎保持不变,如图4.13(a)所示。类似地,当磁场载荷增加时,裂纹面内的磁感应强度增加,对应的电场强度几乎保持不变,如图4.13(b)所示。此外,裂纹面内的电位移和磁感应强度均随着扩展速度的增加而降低。这两个物理量在不同载荷下的区别随着扩展速度的增加而减少。(https://www.xing528.com)
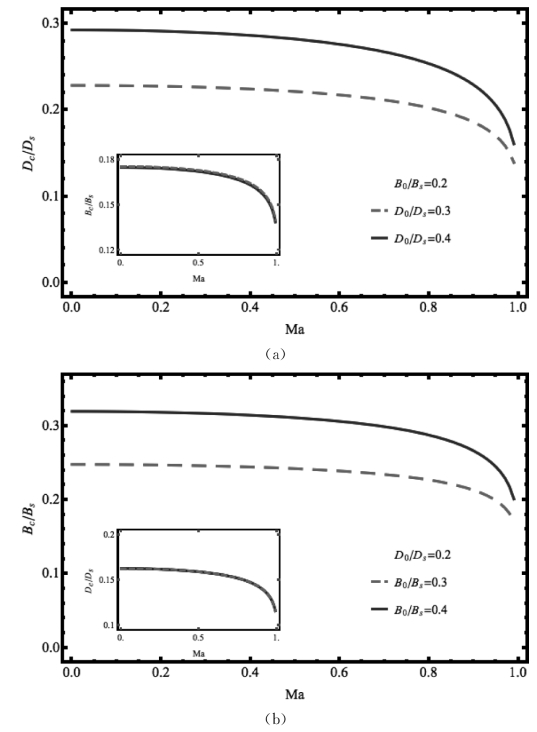
图4.13 Yoffe型磁电弹界面裂纹面内的电场和磁感应强度在不同电磁载荷下关于扩展速度的变化:(a)D0/Ds>B0/Bs(b)D0/Ds<B0/Bs
接下来,讨论电磁屈服的长度在不同边界条件下关于扩展速度的变化。在D0/Ds>B0/Bs情形下,电场屈服长度大于磁场屈服长度,如图4.14(a)和(b)所示。类似地,在D0/Ds<B0/Bs情形下电场屈服长度小于磁场屈服长度,如图4.15(a)和(b)所示。当裂纹扩展速度增加时,电磁屈服区在半导通边界条件下增加,但在绝缘边界条件下保持不变。饱和区的长度在半导通边界条件下比绝缘边界条件下低,并且二者的区别随着扩展速度的增加而减小。
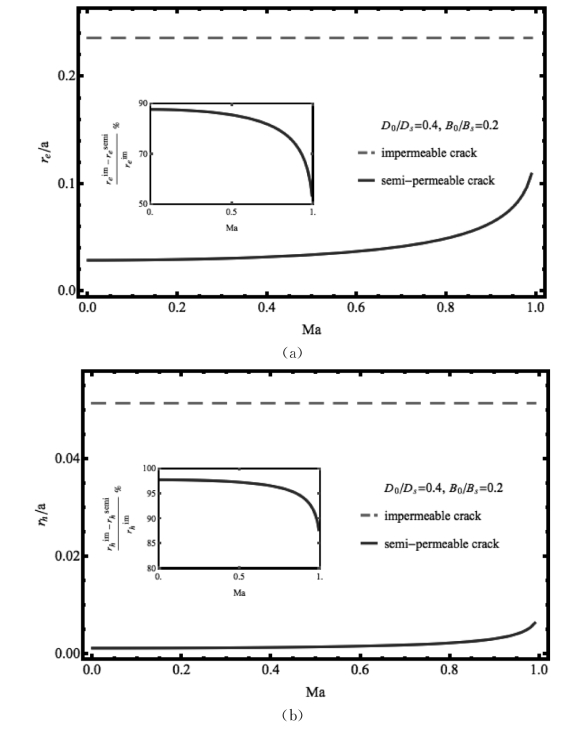
图4.14 当D0/Ds>B0/Bs时,Yoffe型磁电弹界面裂纹的(a)电场和(b)磁场屈服长度在半导通和绝缘边界条件下关于扩展速度的变化(插图表示对应的变化率)
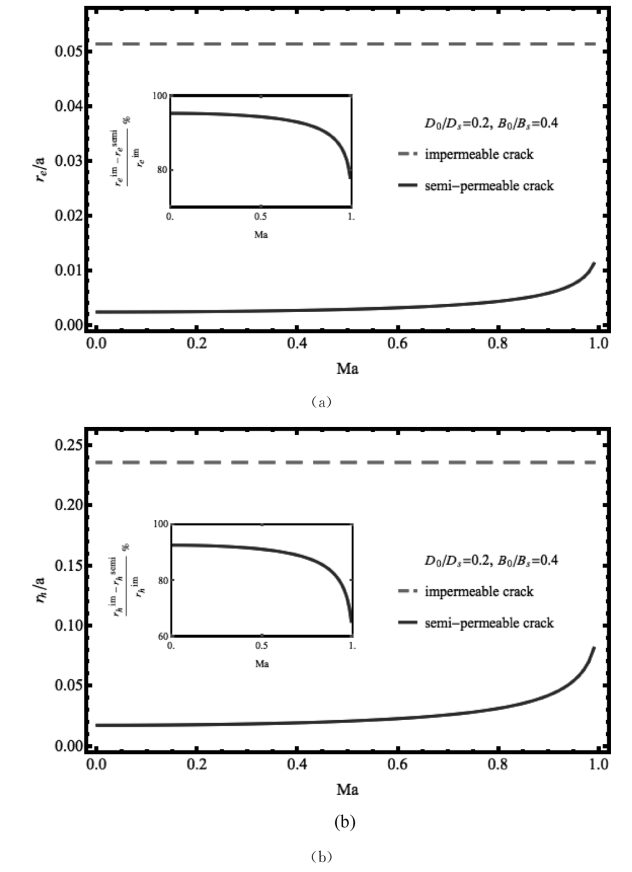
图4.15 当D0/Ds<B0/Bs时,Yoffe型磁电弹界面裂纹的(a)电场和(b)磁场屈服长度在半导通和绝缘边界条件下关于扩展速度的变化(插图表示对应的变化率)。
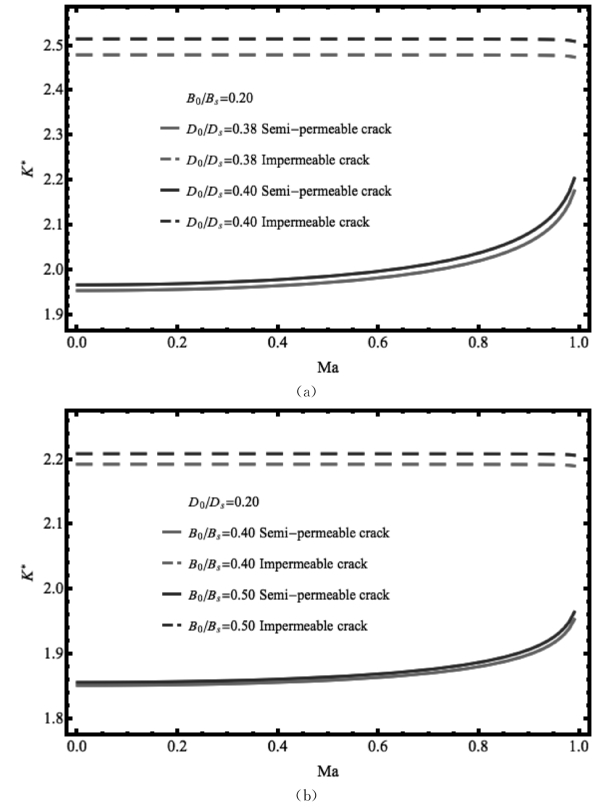
图4.16 Yoffe型磁电弹界面裂纹无量纲应力强度因子在半导通和绝缘边界下分别受到(a)电载荷和(b)磁载荷时关于扩展速度的变化
下面研究断裂控制参数随扩展速度和边界条件种类的变化。图4.16(a)和(b)描述了应力强度因子K*随电磁载荷的增加而增加。在半导通边界条件下,K*在D0/Ds>B0/Bs和D0/Ds<B0/Bs情形下,均随着Ma的增加而增加。相反地,在绝缘边界条件下,K*当Ma远小于1时几乎保持不变。图4.17描述了J*在半导通和绝缘边界下,随着扩展速度的增加而增加。可以看出,由于考虑了裂纹面内的电磁场,断裂控制参数在半导通边界条件下比绝缘边界条件下要低。二者的不同随扩展速度的不同扩展速度的增加而降低,与屈服长度的结论类似。
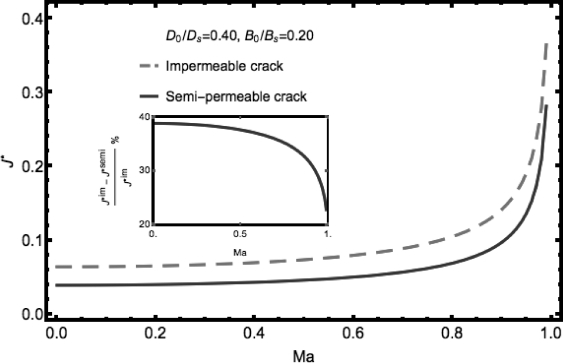
图4.17 Yoffe型磁电弹界面裂纹无量纲能量释放率在半导通和绝缘边界下关于扩展速度的变化(插图表示对应的变化率)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




