求解电磁位错密度控制方程：电屈服与磁屈服比较

本小节中，我们将获得解析形式的广义界面位错。结合方程(4.87)～(4.89)给出弹性界面位错密度的控制方程

其中

方程(4.91)的解为[204]

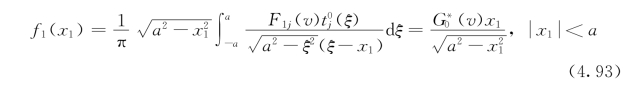
其中

然后，将方程(4.93)带入方程(4.79)，我们获得了界面裂纹内任意点(x1，0)处的位移间断

其中，。注意到，Dc和Bc将在之后被求解。求解电磁位错密度要求电磁屈服区之间的关系。在接下来，两种情况a＜l＜c和a＜c＜l将分别被讨论。

4.3.4.1　电屈服长度大于磁屈服长度(a＜l＜c）

在这种情况下，电磁位错密度的控制方程通过联立(4.88)～(4.89)式获得

其中

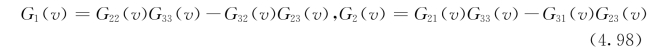
它的解为

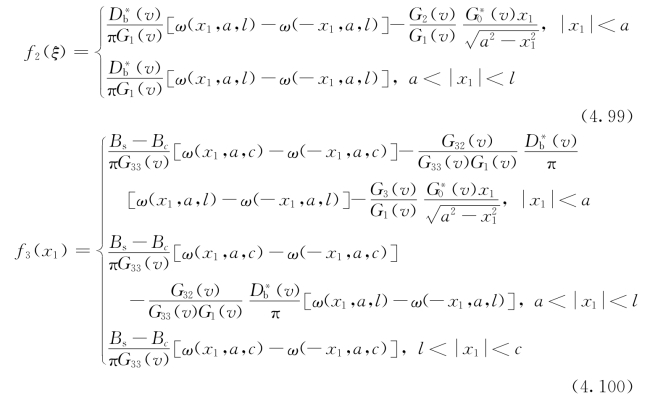
其中

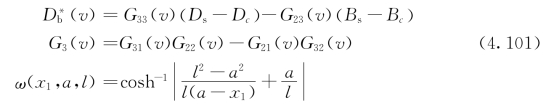
然后，将方程(4.99)～(4.100)带入方程(4.79)，获得了电势及磁势的不连续性

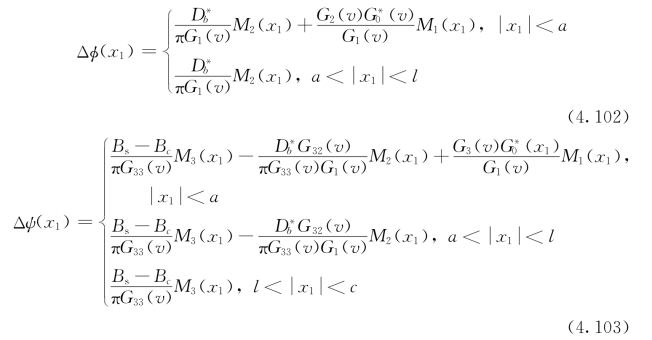
其中

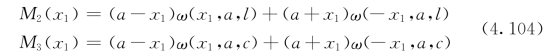(www.xing528.com)

接下来，为了保证电位移在以及磁感应强度在的非奇异性，以下补充方程需要被满足

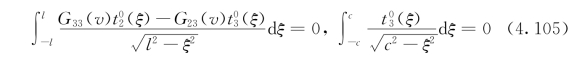
由此给出了电磁屈服区长度

其中，

。

4.3.4.2　电屈服长度小于磁屈服长度(a＜c＜l）

在这种情况下，通过联立方程(4.88)～(4.89)，我们获得了电磁位错密度的控制方程

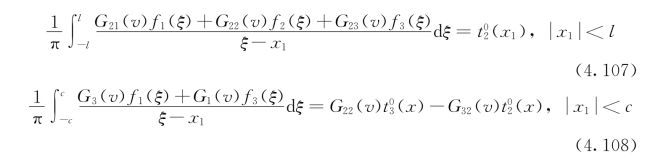
其解为

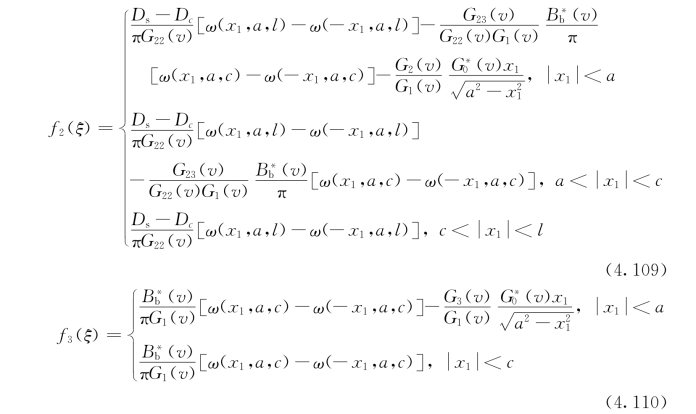
其中，。将方程(4.109)～(4.110)带入方程(4.79)，获得了电势及磁势在裂纹面内的不连续性

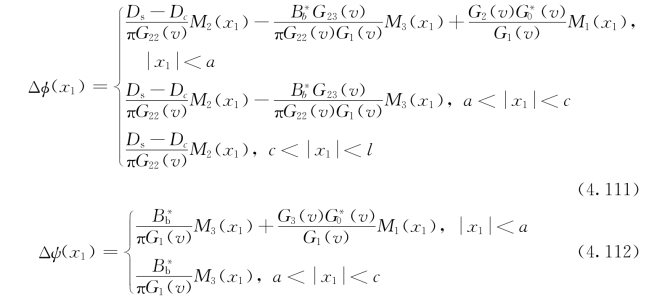
类似地，为保证电位移在以及磁感应强度在具有非奇异性的额外条件是

这给出了电磁屈服区的长度

其中，。

4.3.4.3　裂纹内的电磁场的迭代近似

到现在为止，需要采用迭代近似的方法获得半导通边界条件下，裂纹面内的电位移和磁感应强度。将方程(4.95)中的位移间断，方程(4.102)和(4.111)中的电势间断，和方程(4.103)和(4.112)中的磁势间断带入方程(4.58)中，获得了关于裂纹面内电位移和磁感应强度的隐式方程

最终，Dc和Bc通过Newton法求解方程(4.115)获得。

表4.2 磁电弹复合材料各组份的材料性质[215]