电磁边界条件与条带屈服模型

考虑一个无限大磁电弹双材料，(x1，x3)位于界面平面内。在无穷远处受到反平面力载荷，平面内电位移和磁导率，如图4.10所示。上下两个半平面可以分别用上下标“I”或者“II”来表示。长度为2a的Yoffe型运动界面裂纹以亚声速v在界面上移动。平移坐标系的原点固定在运动裂纹的中央。除了磁电弹固体的控制方程(4.53)，界面裂纹的边界条件也应该给出。在之前的文献中，裂纹面上经常采用力自由的边界条件

其中，上标“＋”和“－”分别表示上下两个裂纹面。裂纹面的电磁边界条件经常采用导通，绝缘或者半导通边界条件。其中，导通边界条件来源于Parton[78]在铁电体中的分析，忽略了裂纹面对电磁场传播的影响。电位移和磁感应强度的法向分量，以及对应的电势和磁势在裂纹面处连续

绝缘边界条件由Deeg[79]在压电体中给出，忽略了裂纹中的电磁场，并假设裂纹面处电磁场法向分量为0

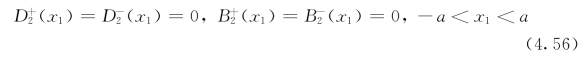
半导通边界条件[81]是指考虑裂纹面内的电磁场，即Dc(x1)和Bc(x1)

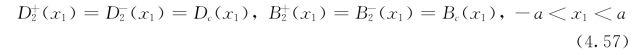
其中，Dc(x1)和Bc(x1)来源于对平面内半导通边界条件的修改

(www.xing528.com)

这里，κc 和μc 分别代表裂纹内物质的介电常数和磁导率，Δϕ(x1)和Δψ(x1)代表电势和磁势的跳跃，Δu3(x1)代表反平面裂纹的位移张开。一般意义上，Ⅲ型界面裂纹不存在裂纹面内的空间。然而，裂纹面一般是非理想的，空气不可避免的存在于上下裂纹面内的微小空间内。半导通边界条件更加符合物理真实情况。注意到，当κc 和μc 取为0时，半导通边界条件可以退化为绝缘边界条件。退化为导通边界条件可以参考Hao和Shen[81]的工作。因此，本节采用半导通电磁边界条件。

由于界面裂纹尖端附近的奇异场，需要考虑裂纹尖端附近的非线性效应。这里我们采用2.2.3小节的动态电磁条带屈服模型。假设力学上脆性并将电磁非线性现象考虑为电位移和磁感应强度在界面裂纹尖端一小段区域内处于饱和状态。

在无穷远处边界条件下很难直接求解方程(4.53)。因此，对磁电弹双材料Yoffe型界面裂纹问题，可以看作是图4.11中两个子问题的叠加，即无界面裂纹的磁电弹双材料受到无穷远处载荷(作用子问题Ⅰ)，以及带有界面裂纹的磁电弹双材料在裂纹面处受到相反方向载荷作用(子问题Ⅱ)。对于子问题Ⅰ，可以得到一个均匀的磁电弹场，与无穷远处载荷相等。对于子问题Ⅱ，界面裂纹的边界条件可以给为

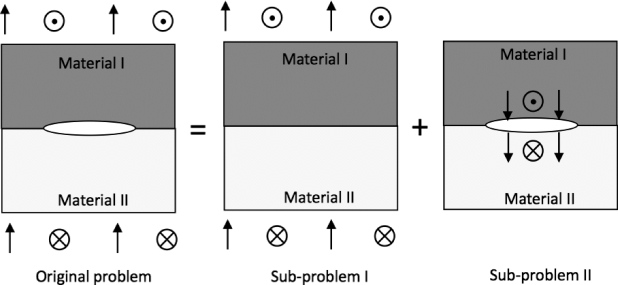
图4.11　两个子问题的线性叠加策略

其中，是裂纹面处外加载荷矢量

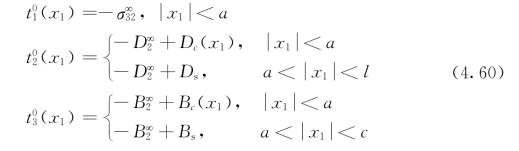
在接下来的部分，我们将重点讨论问题Ⅱ。