【摘要】：在平移坐标系内，反平面问题的平衡方程为其中，是二维拉普拉斯算子。
将一个静止的笛卡尔坐标系
固定在磁电弹固体上，
指向极化方向。动态的磁电弹平衡方程可以给为
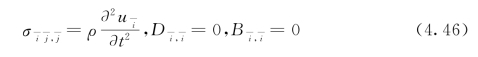
其中，
是密度，位移，应力，电位移和磁感应强度。假设小变形，无体力，无自由电荷，以及无电流密度。这里采用了爱因斯坦求和约定，
代表了对于静止坐标
的偏导数。
一个平移的笛卡尔坐标系(x1，x2，x3)以恒定速度v沿坐标轴
移动，如图4.10所示。这两个坐标系的关系可以写为
图4.10 受到反平面力载荷和平面内电磁载荷的磁电弹双材料Yoffe型界面裂纹问题
因此
将方程(4.48)带入方程(4.46)得到了平移坐标系下的平衡方程(www.xing528.com)
其中，i代表了对于平移坐标xi的偏导数。场变量满足以下线性本构方程
其中，ϕ，ψ，cijkl，elij，hlij，αij，κij，μij分别是电势，磁势，弹性模量，压电系数，压磁系数，磁电系数，介电系数，介磁系数。将方程(4.50)带入方程(4.49)，我们得到了统一形式的平衡方程，
对于一个横观各向同性的磁电弹材料二维问题，面内分量和面外分量是解耦的，广义位移与坐标x3无关，即UK＝UK(x1，x2)。在平移坐标系内，反平面问题的平衡方程为
其中，
是二维拉普拉斯算子。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
