电场调控畴变区域

基于方程(4.10)中的非均匀铁弹－铁电畴变准则，当σDS≥时畴变过程发生。对于某一特定的初始极化方向ϕ，通过设定σDS＝可以得到电场相关的畴变区域

其中，刻画了畴变区域的大小。

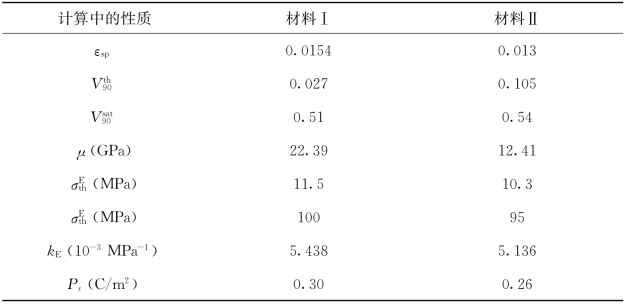
表4.1　当电场消失时铁电复合材料各组分的弹性和畴变系数

此外，通过对高度H 关于φ 求偏导数，可以获得畴变区域的最大高度Hmax(E，ω)

其中

(www.xing528.com)

注意到，的值与电场无关。

结合方程(4.10)和(4.11)，首先可以得到当外加电场为0时的铁弹畴变区域，如图4.2所示。在画图过程中，考虑一个静态界面裂纹，并且设定Kapp＝。材料系数在表4.1中给出。由于双材料各组份材料性质不相同，畴变区域非对称。非均匀畴变区可以分为一个核心的饱和区和渐变的圆环。在核心区内，畴变的体积分数分别保持最大值(在上半区)或者(在下半区)。并且在渐变区域内，V90随着控制变量σDS的降低从饱和值线性减小至临界值。

图4.2　铁电界面裂纹非均匀畴变区域

其次，研究电场对畴变区域的调控。畴变区域的几何形状在铁电-铁弹畴变准则下获得。畴变区域的大小随着正电场的增加而减少(ω ＝0)，随着负电场的增加而增加(ω＝π)，如图4.3(a)和(b)所示。变化趋势与Jiang等[205]的实验结果一致，这表明电场可以调控铁电复合材料畴变区域的几何形状。注意到当上下组份材料性质相同时，结果可以退化至均匀铁电材料铁弹-铁电畴变的情形，如图4.4所示。

图4.3　电场对铁电复合材料畴变区域的调控：(a)ω＝0；(b)ω＝π

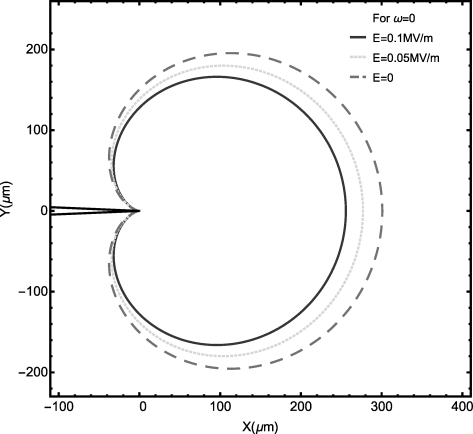
图4.4　电场对均匀铁电体畴变区域的调控