力电耦合场下的畴变过程

考虑一个半无限长的界面裂纹，无穷远处作用有反平面力载荷及平面内电载荷，如图4.1所示。上标“Ⅰ”和“Ⅱ”分别代表上下两个半平面内的铁电组份材料。(x1，x2，x3)表示固定在试件上的全局笛卡尔坐标系，其中原点固定在裂纹尖端。(r，φ)是对应于面内坐标x1－x2的极坐标。此外，笛卡尔坐标系(x′1，x′2，x′3)为固定在铁电单晶上的局部坐标系，如图4.1所示，其中x′3方向沿着初始极化轴以及(x′1，x′2)沿着其他光学轴。

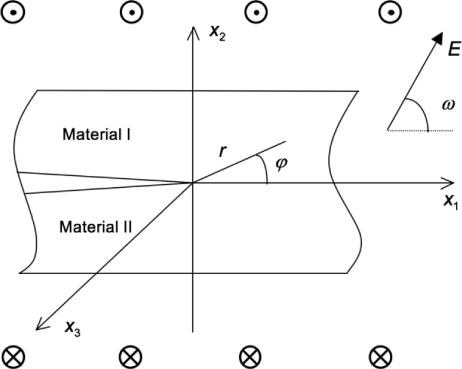
图4.1　铁电双材料半无限界面裂纹在无穷远处受到反平面力载荷和平面内电载荷。

在本节中，假设铁电组份材料弹性和介电性质均为各向同性[196]。这一假设在构建铁电畴变准则时已经被采用[67，154]。力电场的耦合是由于裂纹尖端的畴变过程导致，在畴变区外假设该效应是可以忽略的[196，197]。这里我们关注小范围畴变的情况[198201]，畴变区相比于试件十分小。在此假设下，极化翻转所导致的残余应力可以忽略。所有的畴变应变仅使材料增韧，并不能使材料整体变形发生变化。大范围畴变的工作可参考Cui和Yang[155]以及Cui和Zhong[202]。

Ⅲ型半无限裂纹的复势由Gao给出[203]

其中，Kapp代表远场的应力强度因子。裂纹尖端的应力场可以由复变函数方法获得[204](www.xing528.com)

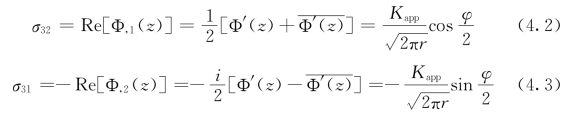
其中，Re[*]代表该参数的实部。应力场的面内分量在小变形假设下为0。此外，在界面裂纹表面采用导通的电边界条件[78]，忽略了由于裂纹缺陷导致的电场扰动[198]。因此，电位移在界面处保持连续。其他电边界条件下的结果[76]可以采用类似的方法进行研究。在面内电载荷和导通电边界条件下，铁电复合材料中的电场可以看做是均匀分布

其中ω代表电场关于x1轴的方向，E 是电场的大小。电场的面外分量为0。为了简化并且不失一般性，假设初始极化方向在平面x1－x2内，并且设定θ＝π/2和ψ＝π/4[157]。(θ，ϕ，ψ)是全局坐标系与局部坐标系间的夹角，如图2.2所示。由方程(2.5)，获得了铁电单晶中实际的畴变功

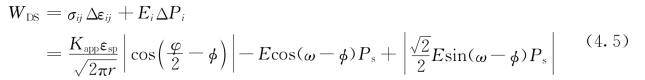
其中，Δεij和ΔPi是铁电单晶中实际的畴变应变和畴变极化强度。注意到，方程(4.5)中WDS的第一项为应力场导致的畴变功，第二项和第三项表示由电场导致的畴变功。此外，实际畴变状态关于极化方向和电场方向的变化在附录B中给出。当电场为0时，方程(4.5)可以退化至铁弹畴变的情况[157]。