首先，我们将计算结果与Zhou和Kamlah[16]非极化铁电陶瓷(PIC151)电致蠕变实验结果相比较。在实验中，PIC151铁电体初始未被极化，并且受到全周期电载荷的加载。非线性D-E 曲线通过方程(3.24)，与演化方程(3.26)来计算。图3.7描述了当电学载荷从0开始增长时，计算所得的非线性D-E 曲线，以及相应的实验数据。在低载荷下D关于E的增长几乎处于线性范围，但很快出现非线性的现象。当载荷达到约为1.0 k V/mm的矫顽场时，曲线开始展现为S形状。超过这个范围后，畴变减慢，并且响应最终回到线性范围。理论曲线整体上与实验曲线相一致。
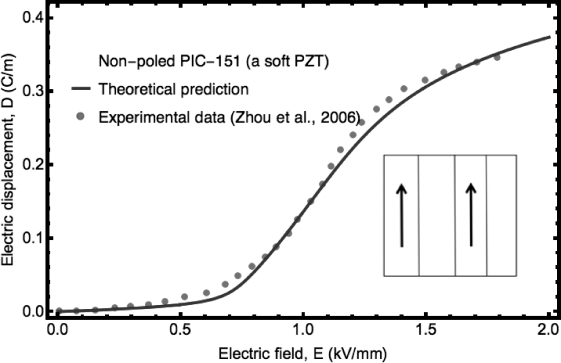
图3.7 非极化铁电陶瓷PIC-151收到正3方向的电载荷时场相关的电位移和电场的关系
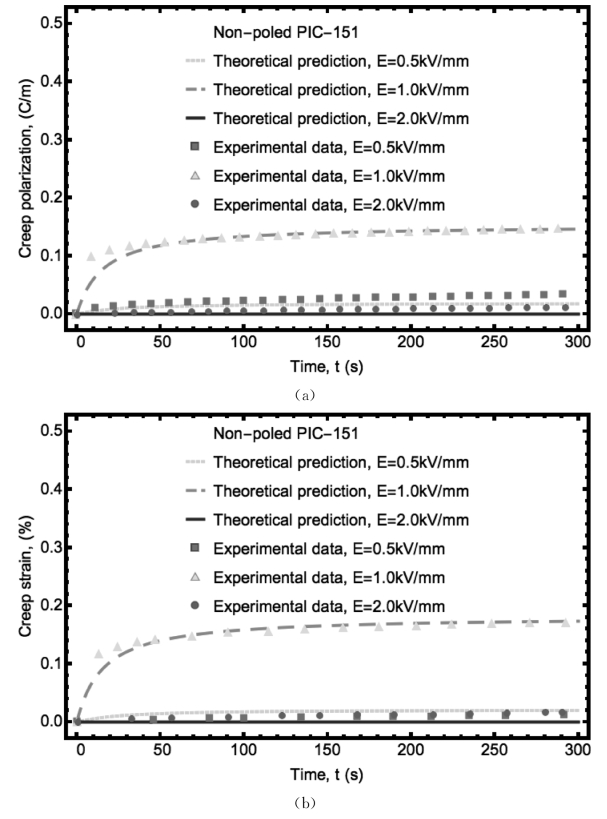
这条曲线可以看做是电致蠕变过程的初始条件。三种电学加载(E ＝0.5，1.0，和2.0k V/mm)可以看做是分别对应三种情况E＜Ec，E＝Ec和E ＞Ec。实验数据与对应时间相关的蠕变计算结果在图3.8(a)和(b)中显示，能够很好的抓住实验现象。计算结果表明，铁电陶瓷的蠕变极化强度和蠕变应变在矫顽场处达到最高，更高的载荷并不能产生更大的蠕变极化和蠕变应变。这一现象表明演化方程通过引入 函数表现出演化过程与加载相关。所有曲线最终达到饱和状态。饱和蠕变极化的最大值发生在矫顽场。这一现象可以归因于在矫顽场附近增加的电致畴变。
(www.xing528.com)
图3.8 非极化铁电陶瓷PIC-151[16]受到恒定电载荷时(a)蠕变极化强度和(b)蠕变应变的演化
计算得到的蠕变曲线是状态变量α和序参数c1演化的结果。这两个变量均和耗散势有着很强的联系。它们随时间的变化关系在图3.9中显示。图3.9(a)表明，在蠕变过程中α从0增长至1。子相体积分数c1随着时间增加而增长，如图3.9(b)所示。其在E＝2.0k V/mm的初始值明显比E＝0.5k V/mm处要高，与图3.7中显示特征相同。图3.9(b)中的插图显示了
随着蠕变过程的进行而下降。
在初始阶段变化很快，然后逐渐降低，最后在平衡状态趋于0。
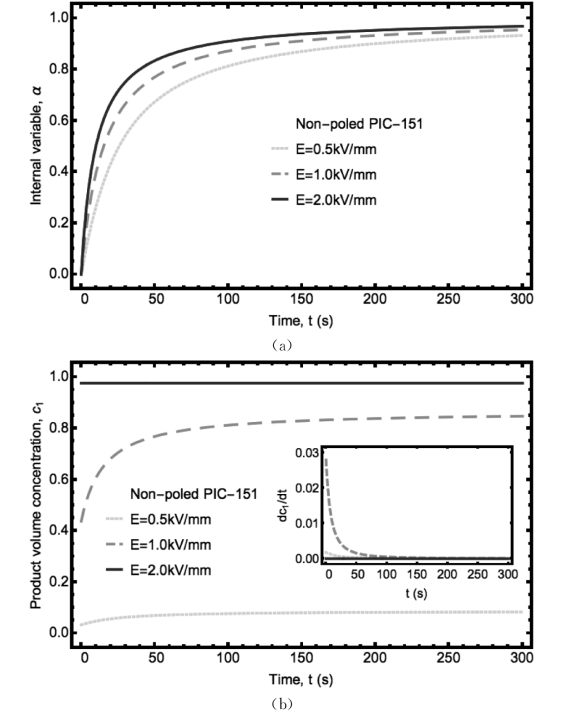
图3.9 非极化铁电陶瓷PIC-151受到恒定电载荷时(a)内变量α(b)子相体积分数c1(插图表示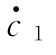
)关于时间的演化
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
