为了导出动力学方程,需要导出双相系统的Gibbs自由能和热力学驱动力。前者可以从下式导出[45,159,177,178]
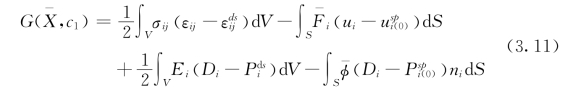
其中,c1为子相的体积分数,![]() 和
和![]() 是父相的瞬时位移和瞬时极化强度,
是父相的瞬时位移和瞬时极化强度,![]() 和
和![]() 指代系统边界上的力载荷和电势。另一方面,参考状态下(即c1=0,无畴变)的自由能为
指代系统边界上的力载荷和电势。另一方面,参考状态下(即c1=0,无畴变)的自由能为
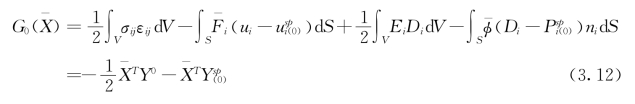
其中,![]() 是由
是由![]() 和
和![]() 施加的外载荷。
施加的外载荷。![]() 指代父相在相同外载下的力电耦合响应。
指代父相在相同外载下的力电耦合响应。
然后,畴变发生后与参考状态间自由能的异质性可以由此给出
![]()
两种状态下自由能的不同最终导致了热力学驱动力。为了获得ΔG 的显式表达式,需要先确定畴结构的形状。对于一般的椭球形夹杂,可以给出[43,45,178,179]
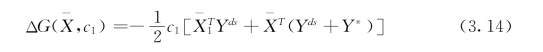
其中![]() 是子相中的平均力电场
是子相中的平均力电场
![]()
并且S是力电场下的Eshelby张量。Yds 和Y*的表达式是
![]()
这里Y*是在夹杂区域用L0代替L1,为了产生相同![]() 而引入的Eshelby形式等效力电本征场。此外
而引入的Eshelby形式等效力电本征场。此外
![]() (https://www.xing528.com)
(https://www.xing528.com)
其中,I是对称的单位矩阵。实验观察可得,BaTiO3畴结构为层状结构[179]。横观各向同性基质中夹杂层状结构的Eshelby张量可在Li[161]的文献中找到。
一种可以代表层状铁电畴结构的特殊椭球形状是平板。这在铁电晶体中的畴结构中经常可以观测到,如图3.4中Merz[180]观察到的BaTiO3畴结构。尽管不能保证沿着晶界都是这样的层状结构,但该结构可以保证最小的能量并且是畴结构中最常见的形态。一般意义上,横观各向同性基质中椭球夹杂的Eshelby张量只能写成积分的形式,圆柱夹杂的显式形式已由Dunn和Wienecke[181]以及Mikata[182]给出。对于层状夹杂Eshelby张量的显式形式已在附录A 中给出。
接下来,通过方程(3.15)~(3.17),畴变过程中Gibbs自由能的变化可以显式给出

图3.4 铁电畴中的层状结构。来自于Merz,Phys.Rev.95,690(1954)。
![]()
其中
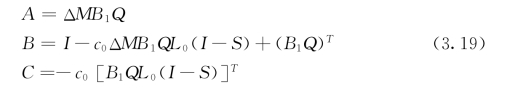
给定外载荷![]() 下的畴变热力学驱动力可以通过对
下的畴变热力学驱动力可以通过对![]() 关于c1求负偏导数给出[43,45]
关于c1求负偏导数给出[43,45]
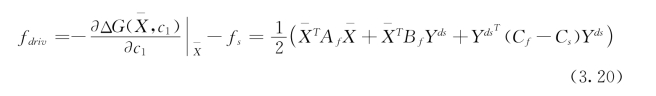
其中
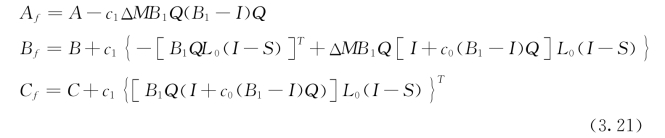
fs是由于去极化场产生的抵抗力。fs必须被减去以提供一个正的驱动力,它可
以被定义为
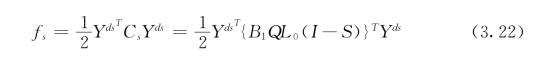
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




