并行边缘检测方法及其应用

边缘检测的方法主要有以下几种：空域微分算子，也就是传统的边缘检测方法，如Roberts算子、Prewitt算子和Sobel算子等；拟合曲面，即利用当前像素邻域中的一些像素值拟合一个曲面，然后求这个连续曲面在当前像素处的梯度；小波多尺度边缘检测；基于数学形态学的边缘检测等。主要介绍空域微分算子，其基本思想是检测每个像素和其直接邻域的状态，以决定该像素是否处于一个物体的边界上。

（一）一阶微分算子

一阶微分算子（即梯度算子）利用灰度一阶导数的信息完成对图像边缘的检测，是一类经典的边缘检测算法，代表性的算法有Roberts、Kirsch、Prewitt、Sobel、Isotropic Sobel、Robinson、Frei和Chen算法等。

如果一个像素落在图像中某一个物体的边界上，则其邻域是一个灰度级变化的带。常用灰度的变化率和方向对这种变化进行描述，它们分别以梯度向量的幅度和方向来表示。一阶微分算子的基本思想是先用近似方法求梯度，然后再取一个阈值，把灰度梯度的幅值大于这个阈值的点作为阶跃状边缘点检出。

图像f（x，y）在像素（x，y）的灰度梯度定义为

其幅值为

方向角为

式中，Gy和Gx别检测垂直和水平边缘。显然边缘在（x，y）处的方向与此点梯度向量的方向垂直。计算图像的灰度梯度，首先要得到每个像素处的一阶偏导数∂f/∂x和∂f/∂y。可用差分来近似表示微分：

1.近似方法

前向差分定义为：

图3-5　像素（x，y）的3×3邻域

用算子分别表示为[-1　1]和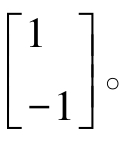 后向差分定义为：

用算子分别表示为[1-1]和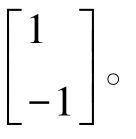

2.Roberts交叉梯度算子

如图3-6所示，其模板表示分别为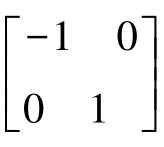和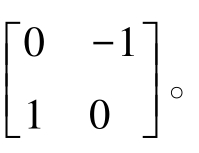 其特点是边缘定位准，对噪声敏感。由于2×2的模板没有清楚的中心点，所以很难直接使用，通常使用3×3的模板。

3.Prewitt算子

即第一行和第三行间的差近似于x方向上的导数，第三列和第一列之差近似于y方向上的导数。如图3-7所示，其模板表示分别为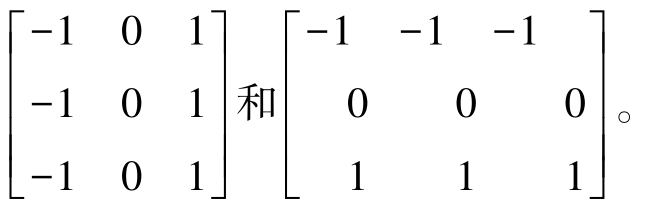

Prewitt算子通过对像素灰度值的平均对噪声起到抑制作用，但是灰度值的平均相当于对图像的低通滤波，所以它对边缘的定位不如Roberts算子。

4.Sobel算子

将式（3-7）Prewitt算子的中心系数上增加一个权值2，得到

图3-6　Roberts算子（a）Gxb）Gy）

图3-7　Prewitt算子（a）Gyb）Gx）

权值2用于通过增加中心点的重要性而实现某种程度上的平滑效果，即Sobel算子。如图3-8所示，其模板表示分别为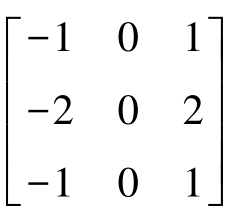和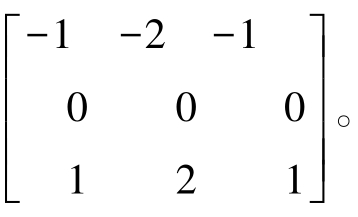有时为了检测特定方向上的边缘，也采用特殊的方向算子，如检测45°或135°边缘的Sobel方向算子分别为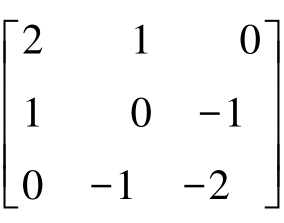和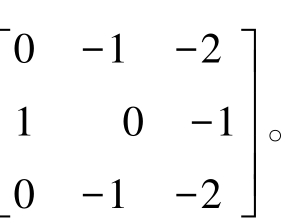

采用Sobel算子检测出的边界宽一般大于或等于2个像素。Sobel算子和Prewitt算子都是采用加权平均算法，但是Sobel算子认为邻域像素对当前像素产生的影响不是等价的，与中心像素距离不同的像素具有不同的权值，对算子结果产生的影响也不同。一般来说，距离越远，产生的影响越小。Prewitt和Sobel算子是在实践中计算数字图像的灰度梯度最常用的算法，前者实现起来比后者更为简单，但后者在噪声抑制特性方面略胜一筹。

图3-6～3-8中，所有模板中的系数总和为0，表示在灰度级不变的区域，模板响应为0。

5.Isotropic（各向同性）Sobel算子

该算子也属于加权平均算子，其权值反比于邻点与中心点的距离，当沿不同方向检测边缘时梯度幅度一致，就是通常所说的各向同性。如图3-9所示，其模板表示为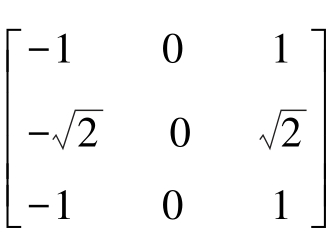和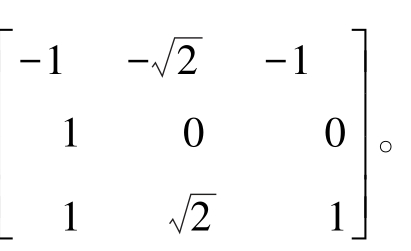和普通Sobel算子相比，它的位置加权系数更为准确。图3-10是分别采用Prewitt算子和Sobel算子对同一幅图像进行边缘检测的结果。

图3-8　Sobel算子

a）Gy　b）Gx

图3-9　Isotropic Sobel算子

a）Gy　b）Gx

图3-10　对Lena图像的边缘检测结果

a）原始图像　b）Prewitt算子处理后的结果图像　c）Sobel算子处理后的结果图像

灰度梯度是一个向量，有大小（见式（3-2））和方向（见式（3-3））。因为在实际中计算梯度的幅值时，平方和平方根的计算量很大，所以经常使用如下两种近似方法：

（二）二阶微分算子(www.xing528.com)

1.Laplacian算子

二维函数f（x，y）的Laplacian算子的定义是：

可以证明Δ2是各向同性的，即

对于一个3×3大小的区域，Laplacian算子的两种常用形式如图3-11所示。

图3-11　Laplacian算子

a）形式1　b）形式2

Laplacian算子不能检测边缘的方向。而且作为二阶导数，它对噪声特别敏感，以至于在边缘检测中无法应用。它的幅值产生双边缘，这是复杂的分割不希望有的结果。基于上述原因，Laplacian算子一般不以其原始形式用于边缘检测。

2.M-H算子

Marr和Hildreth提出的最佳边缘检测算子（简称M-H算子，常称为Marr算子）是将高斯滤波器和Laplacian边缘检测结合在一起，形成了LOG（Laplacian of Gaussian，高斯拉普拉斯）算法。即先用高斯函数对图像进行平滑，然后再用Laplacian算子提取二阶导数的“零交叉”进行边界检测。

二维高斯函数的定义为

对原始图像f（x，y）采用高斯滤波器平滑的结果为

式中，“∗”表示卷积。取高斯滤波器作平滑滤波，可以使频域具有通带窄、空域方差小的最佳特点。用拉普拉斯算子对平滑后的图像进行运算

式中

连接零交叉点的轨迹，就可得到图像边缘。常用的M-H算子是5×5的模板：

M-H是二阶微分算子，具有各向同性，即与坐标轴方向无关，坐标轴旋转后梯度结果不变。噪声点（即灰度与周围点相差很大的点）对边缘检测有一定的影响，而LOG算子把高斯平滑滤波器和拉普拉斯锐化滤波器结合起来，先平滑掉噪声，再进行边沿检测，所以边缘检测的效果会更好。

M-H算子的主要优点如下：

1）该滤波器中的高斯函数部分可以对图像进行平滑，消除图像中尺度变化小于滤波参数σ的噪声或不必要的细节，孤立的噪声点和较小的结构组织将被滤除。而且高斯函数在空域与频域具有相同的形式与性质，都是平滑、定域的，基本上不会引入在原始图像中未出现的变化。

2）用拉普拉斯算子将边缘点转换成零交叉点，通过零交叉点的检测来实现边缘检测，不仅减少了计算量，而且保证了各向同性。

3）滤波参数σ可调，能够在任何需要的尺度上工作。大尺度可以用来检测图像的模糊边缘，小尺度可以用来检测聚焦良好的图像细节。

理论上，边缘点应处在一阶导数的峰值点，在这些点上二阶导数为零，于是可以根据二阶导数过零进行边缘检测。但由于噪声的作用，并非所有二阶导数过零点都对应真正的边缘。如何去掉“假边缘”点，保留真正的边缘点；如何解决抗噪声和边缘定位的准确性这一矛盾；如何选择合适的空间常数，以减少各边缘之间的相互影响，是实际应用中需要解决的问题。

采用不同的边缘检测算子对例图的处理结果如图3-12所示。

图3-12　采用不同的边缘检测算子对例图的处理结果

a）原始图像　b）Sobel算子结果图像　c）Isotropic Sobel算子结果图像　d）M-H算子结果图像

3.Canny算子：

Canny边缘检测算子是Canny于1986年开发出来的一个多级边缘检测算法，他创立了边缘检测计算理论（Computational theory of edge detection）。Canny提出了评价边缘检测算子性能的三个准则：

1）信噪比准则，即良好的信噪比，将非边缘点判为边缘点的概率要低，将边缘点判为非边缘点的概率也要低。

2）定位精度准则，即良好的定位能力，标示出的边缘要与图像中的实际边缘尽可能接近，要尽可能在实际边缘的中心。

3）单边缘响应准则，即对单一的边缘仅有唯一的响应，单个边缘产生多个响应的概率要低，并且虚假边缘要得到最大的抑制。

也就是说，在提高对景物边缘的敏感性的同时，可以抑制噪声的方法才是好的边缘提取方法。基于此，Canny给出了检测阶跃边缘的最佳算子，但计算量非常大。其设计过程如下：

1）首先用高斯滤波平滑图像。

2）利用微分算子，计算梯度的幅值和方向。

3）对梯度幅值进行非极大值抑制。即遍历图像，若某个像素的灰度值与其梯度方向上前后两个像素的灰度值相比不是最大，则这个像素不是边缘。

4）使用双阈值算法检测和连接边缘。即使用累计直方图计算两个阈值，凡是大于高阈值的一定是边缘，小于低阈值的一定不是边缘。如果检测结果大于低阈值但又小于高阈值，就要看这个像素的邻接像素中有没有超过高阈值的边缘像素，如果有，则该像素就是边缘，否则不是。

在并行边缘检测算子中，最简单的是Roberts算子，但它是2×2的模板，没有明确的中心像素，使用不方便。3×3的模板中，Prewitt和Sobel算子是最常用的，前者实现起来比后者更为简单，但后者在噪声抑制特性方面略胜一筹。上述这几种算子都能实现中心定位，但对噪声都比较敏感，尤其是Laplacian算子，它是二阶微分算子，对噪声的放大能力更强于其他一阶微分算子，不利于边缘分析。实用的策略是先对图像进行平滑处理，抑制噪声，再求微分，即为M-H、Canny等算子。若对图像进行局部线形拟合，再用拟合得到的光滑函数的导数代替直接的数值导数，则为Facet模型检测边缘算子。