离散余弦变换及其应用

为了快速有效地对图像进行处理和分析，常通过正交变换将图像变换到频域，利用频域的特有性质进行处理。传统的正交变换多是复变换，运算量大，不易实时处理。随着数字图像处理技术的发展，出现了以离散余弦变换（DCT）为代表的一大类正弦型实变换，它是以实数为对象的余弦函数，均具有快速算法。

DCT是傅立叶变换的一种特殊情况。在傅立叶级数展开式中，被展开的函数是实偶函数时，其傅立叶级数中只包含余弦项，称为余弦变换。虽然DCT没有离散傅立叶变换的功能强大，但是其变换核是为实数的余弦函数，因而计算速度比对象为复数的离散傅立叶变换快得多，计算复杂性适中，又具有可分离特性，还有快速算法。

DCT除了具有一般的正交变换性质外，它的变换矩阵的基向量近似于托普利兹（Toeplitz）矩阵的特征向量，而托普利兹矩阵又体现了人类语音信号及图像信号的相关特性，因此常认为DCT是对语音和图像信号的准最佳变换，已被广泛地用在图像压缩、编码、语音信号处理、信号的稀疏表示等诸多领域中，如JPEG、MPEG-1、MPEG-2及H.261等压缩编码国际标准都采用了DCT编码算法。

（一）一维离散余弦变换

一维离散余弦变换核定义为

式中，x，u=0，1，…，N-1，且

一维离散余弦变换的定义如下：设f（x）是时域的N点序列，x=0，1，2，…，N-1，则其DCT定义为

式中u=1，2，…，N-1是广义频率变量，F（u）是第u个余弦变换系数。显然

将变换式展开整理后可以写成矩阵的形式，即

式中

一维离散余弦变换的逆变换（IDCT）定义为

式中，x=0，1，…，N-1。可见一维离散余弦变换的逆变换核与正变换核是相同的。

傅立叶变换中的指数项通过欧拉公式进行分解，实数部分对应于余数项，虚数部分对应于正弦项。因此，离散余弦变换可以从傅立叶变换的实数部分求得，即离散余弦变换可以改写成以下形式：

式中，u=1，2，…，N-1。对于x=N，N+1，…，2N-1有f（x）=0，Re{·}表示取实数部分，其中求和项就是2N个点上的离散余弦变换。

（二）二维离散余弦变换

可将一维离散余弦变换的定义推广到二维。二维离散余弦正变换的核为

二维离散余弦变换的定义如下：设f（x，y）为M×N的数字图像矩阵，则二维离散余弦变换的定义由下式表示：

上述两式中，x，u=0，1，2，…，M-1；y，ν=0，1，2，…，N-1。F（u，ν）为变换系数矩阵。

二维离散余弦反变换由下式表示：

二维离散余弦变换核是可分离的，因而可通过两次一维变换实现，其算法流程与DFT类似。如图2-17所示，传统的方法是行一列法，即先沿行（列）进行一维离散余弦变换计算，再沿列（行）计算一维离散余弦变换，即

在离散余弦变换中，我们称F（0，0）为直流（DC）系数，其余为交流（AC）系数。图2-18说明了离散余弦变换系数的分布规律。离散余弦变换最主要的特点就是图像经过变换后，主要的能量多数集中在低频系数区域，而图像的细节等信息则分布在中高频区域。因此，在压缩传感中，可以采用离散余弦变换将信号变为稀疏信号，将能量较多的低频系数传输到解码端进行重构。同时，最近的研究还发现，在离散余弦变换域中，图像纹理特征也呈现一定的分布规律。这使得离散余弦变换在图像压缩、特征提取、图像分析，稀疏表示中有着重要的应用。

图2-17　二维离散余弦变换可通过两次一维离散余弦变换实现

图2-18　离散余弦变换频带分布

图2-19是对标准雷娜（Lena）图像进行离散余弦变换前后的结果，可见离散余弦变换矩阵的左上角代表低频分量，右下角代表高频分量。由离散余弦变换域图像能够了解图像主要包含低频成份，如图2-20和图2-21所示。

图2-19　对标准Lena图像进行离散余弦变换前后的结果

a）原始图像　b）离散余弦变换结果(www.xing528.com)

图2-20　对细节较少的图像进行离散傅立叶变换和离散余弦变换前后的结果

a）原始图像　b）离散傅立叶变换结果　c）离散余弦变换结果

图2-21　对细节中等的图像进行离散傅立叶变换和离散余弦变换前后的结果

a）原始图像　b）离散傅立叶变换结果　c）离散余弦变换结果

离散余弦变换在图像的变换编码中有着非常成功的应用。这是由于离散余弦变换是傅立叶变换的实数部分，因而比傅立叶变换有更强的信息集中能力。对于大多数的自然图像，离散余弦变换能将大多数的信息放到较少的系数上，从而提高编码的效率。

（三）离散余弦变换的编程实现方法

对于一维离散余弦变换，首先将f（x）进行补零加长

由于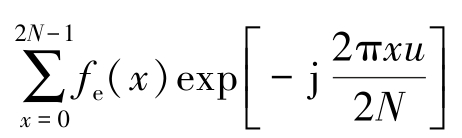为fe（x）的2N点离散傅立叶变换。因此，在做离散余弦变换时，可以通过补零加长的方法，把长度为N的序列f（x）延拓为长度是2N的序列fe（x），然后对fe（x）进行离散傅立叶变换，其实部便是离散余弦变换的结果。同理，对于离散余弦反变换，也可以按照下式延拓F（u）：

按照式（2-149）可得

从上式可见离散余弦反变换可以由的2N点逆傅立叶变换来实现。

对于二维数字图像，离散余弦变换的具体实现步骤如下：

1）获取存储原图像数据的存储区的首地址、图像的高度和宽度。

2）计算进行离散余弦变换的宽度和高度，这两个值必须是2的整数次幂；计算变换时所用的水平方向和垂直方向的迭代次数。

3）逐行或逐列顺序读取数据区的值，存储到新开辟的复数存储区。

4）调用一维离散余弦变换函数进行垂直方向的变换。

5）调用一维离散余弦变换函数进行水平方向的变换。

6）将计算结果转换成可显示的图像。

（四）离散余弦变换的运算量

因为离散余弦变换的计算量相当大，在实用中非常不方便，所以需要研究相应的快速算法。目前已有多种快速离散余弦变换（即FCT），这里介绍一种由快速傅立叶变换的思路发展起来的FCT。

将f（x）通过补零延拓为

按照一维DCT的定义，fe（x）的DCT为

式中，Re{·}表示取复数的实部。由于为为fe（x）的2N点离散傅立叶变换，因此在作离散余弦变换时，可把长度为N的f（x）通过补零延拓为2N点的序列fe（x），然后对fe（x）作离散傅立叶变换，最后取离散傅立叶变换的实部便可得到离散余弦变换的结果。

同理对于离散余弦逆变换（IDCT），可首先将F（u）延拓为

由上式可得，IDCT为

可见，IDCT可由的点的IDFT来实现。