静电力检测实验：测试与应用

1.频移特性表示方法

因为所设计的静电力测量系统是使用探针谐振频率变化来表征静电力变化，需要测量探头和样品之间的距离，z向扫描器使用PZT执行器驱动，使探头尖端以恒定速度接近样品表面。随着探针与测量样品表面的接近，探针和样品之间存在接触的风险，当频移超过阈值时，实验自动结束，并且使得探针与样品表面分离。

由于不能直接测量探头和样品之间的距离，首先，将由PLL电路测量的频移Δf相对于由位移传感器测量的z向扫描器位移z绘制，以研究频移-位移特性。图6.29为使用通过电解抛光制造的钨探针测量的实验结果。

但是，在图6.29中，横坐标轴是z向扫描器的相对位移，而不是探头-样本距离特性。因此，需要使用数学变化方法创建探针-样本距离特性。所获得的距离特性可以由式（6.26）表示如下

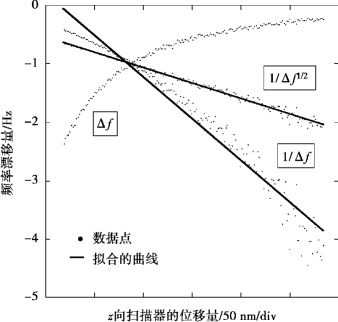
图6.29　探针位移与探针频率变化量（频移）之间的关系图

式中，a，b，n均为常数。

由于z-b对应于探针和样品之间的距离h；b表示样品表面的位置；n是从探头的形状得出的参数。当尖端角较小时，n=2，因为从探针尖端的球形部分接收的静电力是主要的，当尖端角度大时，从侧面接收到的静电力的影响很大，并且该值接近n=1。那么式（6.27）可以表示为

也就是说，如果查看常数n的正确值并绘制函数关系，则可以将测量数据表示为线性函数。如果使用最小二乘法计算式（6.28）的每个系数

把Δfk和zk用作频移的实验数据和位移传感器k点的输出，即

将n=2的数据点绘制在图6.30中。另外，通过最小二乘法将近似直线拟合到每个数据集。已经证实，在电解抛光探针的情况下n=2，可以视为近似的直线关系。

另外，当直接求解b表示样品表面的位置时，从式（6.29）和（6.30）可以得到

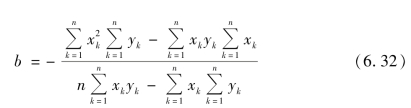
通过电容位移传感器的位移测量结果中减去由式（6.32）获得的b并重新绘制实验结果，可以获得探针频移和探针-样本距离特性曲线。图6.30表示电抛光钨探针的频移与探针和样品之间的距离关系特性曲线。图中上排横坐标值表示探针-样品间距，下排横坐标表示探针位移值。

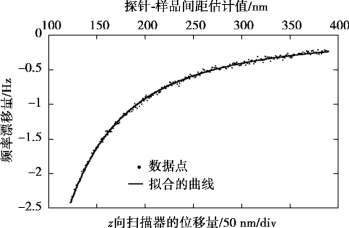
图6.30　探针-样品间距与探针频率变化量（频移）之间的关系图

测量系统的搭建见6.4节的内容。超精密z向扫描器搭载于精密z台上。在z平台上安装平板，并在z方向上移动。通过EFM的力常数（恒力）模式，基于上述测量原理测量该位移。具体的实验步骤如下：

①给z向扫描器设置一个位移确定值。

②给出频移setf的设定值。

③在频移恒定反馈结束后，记录z向扫描器的位移d a和检测到的频移f a。

④更改频移setting-f的设定值。

⑤稳定后，记录z向扫描器的位移d b和检测到的频移f b。(www.xing528.com)

⑥从公式（6.26）计算探针到样品的距离h，并用d a+h计算z级的位移。

通过重复上述过程绘制校准曲线，取水平轴上的z平台的位移和垂直轴上的计算位移。

从实验中获得的校准曲线如图6.31所示。在该实验中，f的设定值设定为0.95 Hz和0.76 Hz。计算的探针与样品距离h均约为100 nm。绘制的校准曲线可以用直线很好地近似，并且线性近似的标准偏差是3.8 nm。因此，可以预计EFM的形状测量结果将包括z方向上标准偏差约为3.8 nm的变化。

图6.31　校准曲线

2.不同材料上的频移测量实验

使用不同类型非导体（绝缘体）进行初步检测实验，绘制频移和探针-试样间距关系图可以初步验证系统对不同材料测量的有效性。

从式（6.26）可以看出，探针频移值Δf也是试样材料介电常数εr的函数，这就意味着频移会受到材料的影响。使用6.4节所搭建的EFM系统测试了探针频率随着探针尖端和不同电介质上的样品表面之间不同距离的变化关系。

首先，采用K9玻璃作为样品，使用铝合金作为背电极。在探针尖端和后电极之间施加的偏置电压为100 V。在该实验中，探针以谐振器的基频振荡，该频率约为26 546 Hz，振荡系统的品质因数为2 832。样品保持静止，通过z向扫描器移动探针尖端接近样品表面，研究频移与尖端到样品距离之间的关系。其结果如图6.32所示。纵坐标表示相应的频移值，底部横坐标表示z向扫描器的位移输出，即z扫描器的相对位移。通过使用最小二乘法可以用一个逆三次函数很好地拟合结果，逆立方拟合曲线可用于基于式（6.26）估计探针尖端到样本表面的距离。在图6.32中，上面的横坐标是通过最小二乘法拟合的估计出的探针尖端到样品表面的垂直距离。

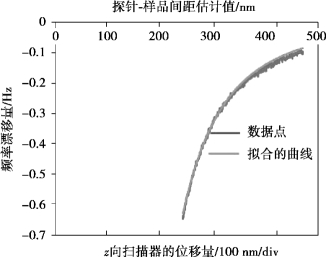
图6.32　在玻璃试件上测量的d和Δf之间的关系曲线

然后，采用相同的步骤，将硅片和PVC膜作为样品并分别进行测试。图6.33和图6.34是在该两种试样上的测试结果。

图6.33　在硅试件上测量的d和Δf之间的关系曲线

图6.34　在PVC试件上测量的d和Δf之间的关系曲线

由图6.32、6.33和6.34可以看出上述3种类型的材料均可以通过EFM系统进行测试，探针所受静电力随探针针尖与试件之间的距离减小而增大，探针单元谐振频率则随之减小，其变化关系和式（6.26）相吻合。但是，对PVC材料进行测量时，探针频率变化量Δf的变化最小，这是因为PVC材料的介电常数εr最小。

3.不同试件位置的探针频移测量实验

为了反映试件形状对扫描测量的影响情况，采用一个具有高25μm，45°斜面的衍射光栅作为测试样品进行静电力检测实验。图6.35为样品的表面形貌，其中右图是斜面部分试件的截面形状。

图6.35　含45°斜面的试样显微图

实验时，首先选定试样任意位置，保持试样不动，移动z向扫描器，检测探针频率变化量，直到其设定的阈值，根据检测结果绘制频移-间距（探针尖端和试样表面之间的垂直距离）关系图。然后，在试样表面，沿着x方向（图6.36中的水平轴方向），在50μm（试样形貌的一个周期长度）长度内，通过x向扫描器以1μm步长移动50次，测量50个点，这样可以确保测试了形貌上的顶部、谷点和斜面任意部位（如图6.36所示）所有点，可以描绘出每个位置的频移-间距关系曲线。图6.37给出了其中的3个，它们分别是顶部，坡度中间和谷部。在图6.37中，平滑曲线是拟合曲线，粗曲线是测试实际曲线。由图6.37的数据可以看出，在不同的三个位置，频率变化情况基本一致，不同位置测量值之间的最大误差约为6 nm，即为扫描测量时的最大误差值。同时，该测量结果也反映了对于相同材料的试件，测量位置的试件厚度对测量值基本没有影响。

图6.36　试件上不同位置进行频移特性曲线测量示意图

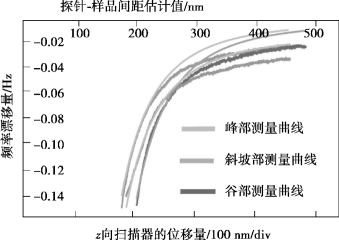
图6.37　试件上不同位置频移-距离关系曲线