柔性微杠杆机构的分析与优化方法

1.一级柔性微杠杆结构类型

柔性微杠杆机构是一种部分柔性机构，是将普通杠杆的铰链用柔性杆（柔性铰链）代替，具有传递、放大（缩小）力和位移的作用，在微机械领域具有广泛的应用前景。考虑微机械加工工艺特点，在MEMS中可以将柔性铰链微杠杆设计成如图5.20所示的8种形式。图5.20中（a）、（b）、（c）和（d）的四种结构，均为柔性支撑杆（柔性铰链）位于杠杆中部，而输出端和输入端则分别位于柔性铰链的两侧；图5.20中（e）、（f）、（g）和（h）的四种结构，均为柔性支撑杆（柔性铰链）位于杠杆一侧，而输出端和输入端则位于柔性铰链的同侧。因为需要考虑杠杆臂（假设为刚性杆）宽度对其力传递系数的影响，故图5.20中（a）、（b）、（c）和（d）四种情况有所区别，同样，（e）、（f）、（g）和（h）四种结构也不相同。

图5.20　不同类型的一级微杠杆机构

2.柔性微杠杆传力系数分析

下面举例分析微杠杆机构的传力系数。选择图5.20（d）中所示的微杠杆结构来进行分析，其力学模型可简化为图5.21所示。

图5.21　柔性微杠杆的力学模型

图5.21（a）柔性微杠杆结构和变形示意图，杠杆臂（可以看成刚体）被柔性铰链支撑，当杠杆一端有输入载荷（F in）时，柔性支撑杆变形，杠杆另一端输出（F out）。为了研究输入和输出之间的关系，将柔性支撑杆和输出端柔性杆分别简化为两个拉伸弹簧和扭转弹簧，如图5.21（b）所示。对杠杆进行受力分析，其受力图如图5.21（c）所示。由于微杠杆尺寸均处于微米量级，可以不考虑尺寸效应对其影响，那么使用材料力学理论分析其变形和力之间的关系，则杠杆的平衡方程、物理方程和变形协调方程分别为

解上述方程组可得杠杆的传力系数A（输出力与输入力之比）为

式中，

分别为柔性支撑杆和输出端柔性杆的轴向抗拉（压）刚度；

(www.xing528.com)

分别为柔性支撑杆和输出端柔性杆的横向抗弯刚度；

为柔性支撑杆和输出端柔性杆的横截面面积；

为柔性支撑杆和输出端柔性杆的截面惯性矩。

b p，h p，l p和b o，h o，l o分别为柔性支撑杆的厚度、宽度、长度和输出端柔性杆的厚度、宽度、长度。

设计柔性铰链微杠杆的最主要目标是得到最大的传力系数，以下分析柔性杆各参数与传力系数之间的关系。

假设整个结构厚度尺寸相同，均为b=30μm；材料弹性模量E=0.169 N/μm2；输入端杠杆臂（动力臂）长L in=100μm；输出端杠杆臂（阻力臂）长L out=10μm。根据式（5.1）则可以得到柔性支撑杆几何参数与传力系数（A）之间的关系，其关系可以表示为图5.22和图5.23。由图5.22和图5.23可以看出，杠杆传力系数并不是随柔性支撑杆的刚度减小一直增大，当柔性支撑杆宽度在2～4μm、长度在30～50μm时，杠杆有最大传力系数。同样方法，图5.24和图5.25为微杠杆传力系数A与输出端柔性杆几何参数之间的关系。可以看出，杠杆传力系数随输出端柔性杆的宽度增大而减小，当其长度在20μm以下时，传力系数随长度变化明显，但当其长度在20μm以上时变化不明显。

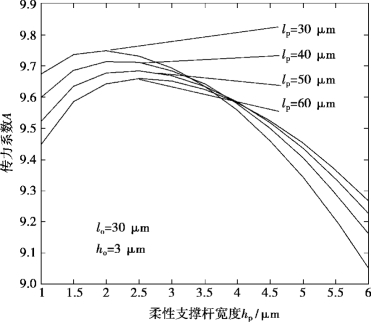
图5.22　传力系数与柔性支撑杆宽度之间的关系

图5.23　传力系数与柔性支撑杆长度之间的关系

图5.24　传力系数与输出端柔性杆宽度之间的关系

图5.25　传力系数与输出端柔性杆长度之间的关系