石英晶体（板式）谐振子的有限元分析

石英晶体是一种天然的性能良好的谐振材料，被用来制作各种谐振敏感元件，常用的结构有音叉式、平面式等。在设计石英晶体谐振器时，需要考虑电极几何参数、晶体结构及几何参数等对谐振器谐振频率的影响。这些参数主要包括电极形状、位置、尺寸和晶体的形状、几何尺寸等。另外，还需要分析晶体夹具设计和周围介质等对晶体谐振频率的影响等。这就需要对晶体结构进行机电以及多物理场的耦合分析，而目前理论研究大多利用解析和半解析的方法将问题近似为一维或二维模型，对材料常数作近似处理，进行简单的近似分析。为了精确设计晶体谐振器，需要对晶体谐振器的模态和频率进行准确分析，下面为使用有限元法对平面式石英晶体谐振器高阶模态进行分析的案例。

（1）建立几何模型的“等效密度法”

平面式石英晶体谐振器结构如图3.32所示，由AT切石英晶片和在晶片上下表面制作的两个电极构成。

图3.32　平面式石英晶体谐振器

在建立有限元模型时，由于电极层厚度100 nm与晶片厚度0.272 mm相比很薄，若对其直接建模，有限元的单元尺寸需设置得很小（至少小于100 nm），这样会导致计算量太大，影响计算效果。为了减少自由度数，节约计算资源，需对电极区使用“等效密度法”进行处理。考虑到电极对系统的影响主要表现在降低了厚度剪切模态的基频，使系统呈现“能陷效应”。因此，只要保证模型对基频的影响不变，就能正确地反应系统的“能陷效应”。假设电极随晶片表面做刚体运动，对于非电极区，其基频为

而电极区的基频为

式中，，ρe为电极密度；

t e为电极厚度；

ρ为石英晶体密度；

t为晶片厚度。

式（3.97）可改写为

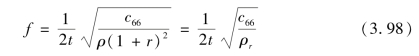
这里的ρr=ρ（1+r）2，称为“等效密度”。这样使得电极区与非电极区的差别仅在于密度不同，而厚度相同，从而便于单元划分。所建立的有限元模型如图3.33所示。

(www.xing528.com)

图3.33　晶振片有限元分析模型

将夹具的夹紧件简化为圆环，所用材料选择聚四氟乙烯橡胶，一面与晶振片接触，另一面固定，包含夹具的有限元模型如图3.33（b）所示。

（2）边界条件及材料参数确定

晶体谐振片的夹具为橡胶密封圈，橡胶与石英晶片的固有频率相差105以上，而橡胶与晶片间的夹持力很小，因此，在有限元分析时将晶片的边界条件简化成自由边界。

AT切割石英晶体的力学和电学特性为各向异性，材料弹性系数矩阵为c ij；压电系数矩阵为

介电常数矩阵为

（3）计算结果

利用上述有限元模型，计算石英晶体谐振器在膜厚为0～50μm情况下振动模态，图3.34为谐振器前六阶（低频时）模态的振型图。可以看出，该分析结果与参考文献[33]中通过实验方式采集到的振动模态基本一致，说明了该有限元模型和分析结果是有效的。

高频厚度剪切振动谐振频率的计算结果见表3.3。高阶厚度剪切振动的模态如图3.35所示。

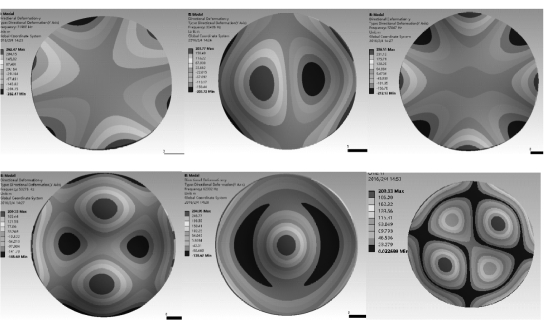
图3.34　谐振器低频振动时的前六阶模态图

表3.3　不同膜厚下谐振器频率的有限元分析结果

图3.35　谐振器高频厚度剪切振动模态