弹性梁振动方程优化

首先考虑细长梁的横向弯曲振动，如图3.1所示。假设梁的各截面的中心主惯性轴在同一平面xOy内，外载荷也作用在该平面内，梁在该平面内做横向振动，这时梁的主要变形是弯曲变形，在低频振动时可以忽略剪切变形以及截面绕中性轴转动惯量的影响，这种梁称为伯努利-欧拉梁（Bernoulli-Euler Beam）。

建立如图3.1所示的坐标系，设y（x，t）是梁上距原点x处的截面在时刻t的横向位移，p（x，t）是单位长度梁上分布的外力，m（x，t）是单位长度梁上分布的外力矩，记单位体积梁的质量为ρ，梁的横截面积为A，材料弹性模量为E，截面对中性轴的惯性矩为I。图3.1（b）画出了微段d x的受力情况，其中Q、M分别为截面上的剪力和弯矩，是微段的惯性力，图中所有的力和力矩都按正方向画出。则其横向弯曲振动微分方程可表示为

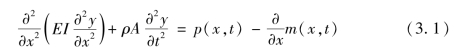
对于等截面梁，其抗弯刚度EI为常数，式（3.1）可写为

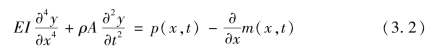
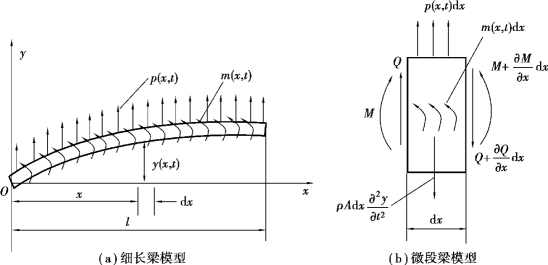
图3.1　伯努利-欧拉梁横向振动力学模型

在式（3.2）中令p（x，t）=m（x，t）=0，得到梁的横向弯曲自由振动方程为

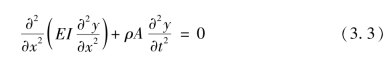
可以将梁的主振型假设为

对于等截面梁，式（3.3）可写为

其中

那么梁的主振动可表示为

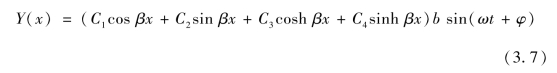
其中，常数C1、C2、C3、C4及固有频率ω由边界条件及主振型归一化条件确定，常数b和φ则由初始条件确定。

梁的两端共有四个边界条件，常见的简单边界有下列几种：

①固定端

在梁的固定端上挠度y与转角都等于零，即

②简支梁

在梁的简支端上挠度y与弯矩M等于零，即(www.xing528.com)

③自由端

在梁的自由端上弯矩M和剪力Q等于零，即

上述各个边界条件中，反映对端点位移或转角约束情况的称为位移边界条件，反映对端点弯矩或剪力约束情况的称为力边界条件。由式（3.8）、（3.9）及（3.10）看到，既不存在挠度与剪力同时为零的情况，又不存在转角与弯矩同时为零的情况。当挠度为零时，挠度受到了限制，必然有剪力产生；反之，剪力为零时，挠度必然是任意的，转角与弯矩的关系也是如此。所以，对于梁的简单边界，总是挠度或剪力中的一个与转角或弯矩中的一个同时为零。

对于两端固定梁的边界条件

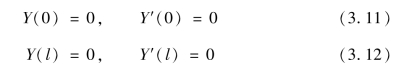
可以得到频率方程为

由方程（3.13）可以求得前四个根的数值解为

当i≥3时频率方程可以近似写为cosβl≈0，则有

由式（3.6），固有频率可以表示为

其中基频为

各阶模态函数为

式中

图3.2为双端固定梁前三阶振型。

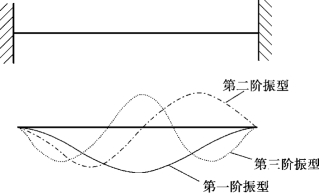
图3.2　双端固定梁前三阶振型