能量关系在谐振状态下的研究

谐振系统在外界施加激励做强迫振动时，激励力对谐振子做功，能量不断输入振动系统。当每周期的能量输入与每周期的能量消耗相等时，能量相互抵消，谐振子振幅将保持常值，系统进入稳态振动状态。但将激励力去掉后，谐振子不会马上停止振动，而是随时间以自身的固有频率不断做衰减运动。简言之，此谐振系统具有储存能量的能力。下面从能量的角度，对输入能量、耗散能量和储存能量之间的能量变换进行分析，得到谐振子在谐振状态下的能量关系。

（1）输入能量与耗散能量

假设稳态振动时的激励力为f=F sin ωt，谐振系统随之做简谐振动，其做简谐振动速度为，通过如图2.4所示的机械系统等效模拟图可得系统在一个周期内的输入能量，即谐振系统激励力在一个周期内所做的功可表示为

当，此时系统处于谐振状态，Wf取得最大值

同理可得，黏性阻尼Fc所引起的系统在一个周期所耗散的能量为

由式（2.23）可得到F=Fc，因此

因此，可证明有激励力F输入系统的能量等于谐振时系统阻尼力Fc引起的耗散能量。

（2）输入能量和储存能量

参振质量m和弹簧k是谐振系统中的储能元件，在系统稳态谐振时，它们在任意瞬时储存的能量分别为

式中，Wm为参振质量m的动能；

Wk为弹簧k的变形能。

两者之和为谐振系统瞬时储存的总能量

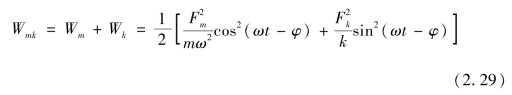
由于系统谐振时，存在，故得到

由上式可得出谐振系统瞬时的总能量为

由式（2.31）可以看出，存储在参振质量m中的动能和弹簧k中的变形能之和是与时间t无关的常量。

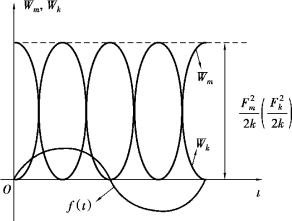
图2.7所示为动能Wm和变形能Wk随时间t的变化曲线。由图可以看出，存储在参振质量m上的动能和弹簧k上的变形能最大值均为，这表明了系统谐振时的总能量为一常量，且其大小恰好等于这个最大值。当动能Wm增大某一数值时，变形能Wk就必然减少同样大小的数值，反之亦然。简言之，系统发生稳态谐振时，参振质量m的动能和弹簧k变形能的变化过程就是一个能量不断相互转换的周期振荡过程，无论振荡过程的振动情况如何，它们之间没有能量传递给激励器，也不会从激励器中吸收能量。这也说明了，激励器仅提供系统阻尼所耗散的那部分能量，与储存能量无关。

(www.xing528.com)

图2.7　能量变化曲线图

为更好地描述谐振系统的能量特性，引入谐振系统谐振子的品质因子Q的能量定义，即每个周期储存的能量与阻尼消耗的能量之比。又由于每个周期耗散的能量等于每周期激励器输入的能量，所以该定义实际上表征了单位输入能量Wf产生振系的动能Wm和变形能Wk大小的能力。

谐振系统谐振子的品质因子Q的能量定义可表示为

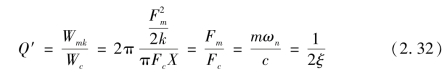
所得结果与上文所表示的谐振系统谐振子的品质因子Q相同，这表明稳态谐振时，系统储存的能量为激励器输入能量的Q倍。

由式（2.32）以及激励力F和阻尼力Fc的关系可得，式（2.31）可表示为

因此，由式（2.33）可得，谐振系统储存能量的总和Wmk与品质因数Q的平方成正比，在激励力一定的情况下，Q值越大，系统储存的能量也越大，振荡的程度就越剧烈。

综上所述，由阻尼器、弹簧及参振质量所构成的谐振系统，实质上就是系统内部能量相互转换的过程。如果排除系统在谐振过程中的能量转换损失，那么系统中参振质量的动能与弹簧的变形能之和将保持不变。其中，激励力所做的功仅仅弥补了系统在谐振过程中由阻尼所引起的能量损失。而激励力的大小，则决定了系统内部惯性动能与弹性变形能相互转换的幅度。

（3）能量传递速率（功率）

对于任意时刻，激励力传输给质量、弹簧以及阻尼器能量的速率为

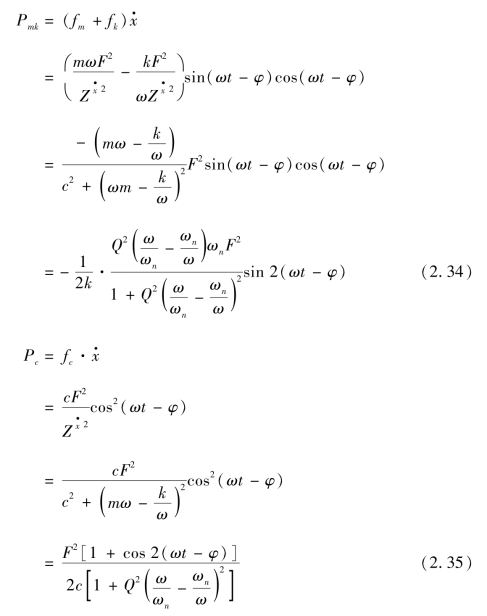
由上式可得，当ω=ωn时

在激励器与储能元件之间没有相互能量交换时，阻尼器的能量输入速度达到最大，即

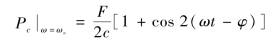
换句话说，此时激励器与阻尼器之间以最大、最快的速率进行能量交换。

激励器输送给谐振系统的总功率的分配可表示为

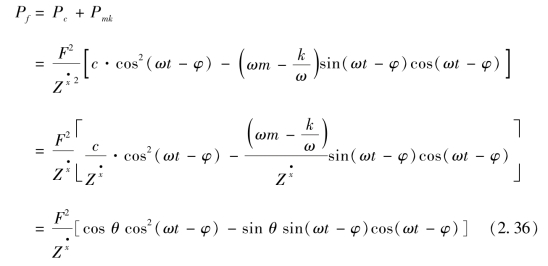
式（2.36）中，cosθ为有功功率因数，sinθ为无功功率因数。

当谐振时，sinθ=0，cosθ=1，激励器的输出功率等于阻尼器的输入功率。可见，谐振的实质就是系统有用功率因数为1的状态，同时也表明了激励器在谐振时对系统的输出功率达到最大，此时激励器与谐振系统进行了最大的能量交换。

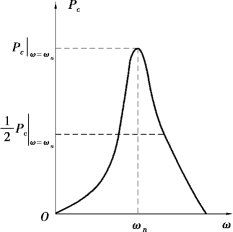
图2.8　阻尼器平均输入功率曲线示意图

而当偏离谐振状态时，阻尼器的输入平均功率将急剧下降，其变化趋势如图2.8所示。