谐振状态下的动力学特性

在机电相似变换的基础上，考虑到谐振系统在谐振时各元件的受力情况，由图2.4所示的机械系统等效模拟图，可得到任一频率各支路稳态力的方程为

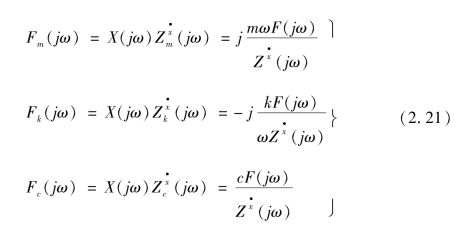
其幅值为

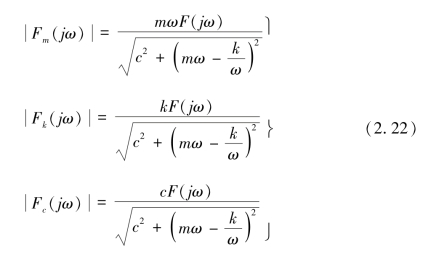
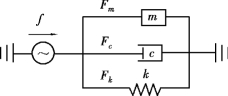
图2.4　谐振式传感器机械系统等效模拟图

当机械系统发生谐振时，即时

根据式（2.22）、（2.23），可以得出如图2.5所示的各支路受力幅频特性关系曲线，表示了谐振系统中各元件的受力情况。(www.xing528.com)

由以上的推导过程及结果表明，当振子发生谐振时：

①弹性力Fk与惯性力Fm大小相等，方向相反，相互平衡；激励力F与阻尼力Fc大小相等，方向相反，相互平衡，且两对平衡力互相正交。构成如图2.6所示的平面正交力系。

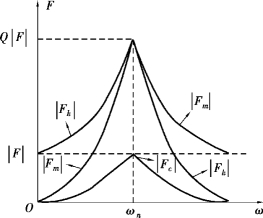
图2.5　各支路受力幅频特性关系曲线图

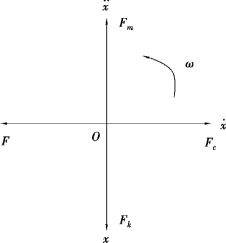
图2.6　平面正交力系示意图

②激励力F仅被用于平衡系统的阻尼力Fc。如果减小系统阻尼，即可使得激励力F减小，且可获得同样的振动效果。

③惯性力Fm和弹性力Fk为激励力F的Q倍。因此，系统的品质因数可以表征在单位激励力作用下，使参振质量m产生的惯性力大小的能力。其中，式（2.20）仅说明了系统谐振时，惯性力与激励力之间的数值关系。但实际上两种力的性质完全不同，所以惯性力不能简单地认为是激励力的放大。

④虽然惯性力Fm和弹性力Fk，与激励力F和阻尼力Fc之间是正交关系，但并不能够表示两者之间相互独立，没有关联。根据式（2.23）可知，若系统的品质因数Q确定不变，则一定量值的激励力F对应着一定量值的惯性力Fm或弹性力Fk。