传感器动态特性分析

传感器的动态特性是指其输出对随时间变化的输入量的响应特性。一个动态特性好的传感器,其输出将再现输入量的变化规律,即和输入量具有相同的时间函数。实际上输出信号不会与输入信号具有相同的时间函数,这种输出与输入间的差异就是所谓的动态误差。

以动态测温为例,如图2.15所示,设环境温度为T0,水槽中水的温度为T,而且T＞T0,将传感器突然插入被测介质中;用热电偶测温,在理想情况下测试曲线的输出值是呈阶跃变化的,而实际上热电偶输出值是缓慢变化的,存在一个过渡过程。

图2.15　测温

造成热电偶输出波形失真和产生动态误差的原因是温度传感器有热惯性(由传感器的比热容和质量大小决定)和传热热阻,使得在动态测温时传感器输出总是滞后于被测介质的温度变化。这种热惯性是热电偶固有的,这决定了热电偶测量快速温度变化时会产生动态误差。

动态特性除了与传感器的固有因素有关之外,还与传感器输入量的变化形式有关。

1.传感器的动态数学模型

要精确地建立传感器(或测试系统)的动态数学模型是很困难的。在工程上常采取一些近似的方法,忽略一些影响不大的因素。

传感器系统(线性时不变系统)的方程为

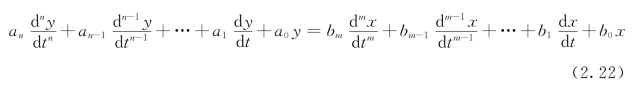
其中,an,an-1,…,a0和bm,bm-1,…,b0均为与系统结构参数有关的常数。在信息论和工程控制中,通常采用一些足以反映系统动态特性的函数,将系统的输出与输入联系起来,这些函数有传递函数、频率响应函数和脉冲响应函数等。

(1)传递函数

设x(t)、y(t)的拉氏变换分别为X(s)、Y(s),对式2.22两边取拉氏变换,并设初始条件为零,得

其中,s为复变量,s=b+jω,b＞0。

定义Y(s)与X(s)之比为传递函数,并记为H(s),则

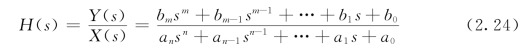
因此,研究一个复杂系统时,只要给系统一个激励x(t)并通过实验求得系统的输出y(t),由H(s)=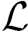[y(t)]/[x(t)]即可确定系统的特性。

(2)频率响应函数

对于稳定系统,令s=j,得

其中,H(jω)为系统的频率响应函数,简称频率响应或频率特性。

将频率响应函数改写为

其中,

称为传感器的幅频特性,表示输出与输入幅值之比随频率的变化。

称为传感器的相频特性,表示输出超前输入的角度,通常输出总是滞后于输入,故其总是负值。研究传感器的频域特性时主要用幅频特性。

(3)冲击响应函数

单位脉冲函数d(t)的拉氏变换为

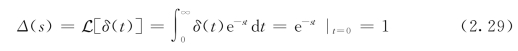
故以d(t)为输入时系统的传递函数为

再对式(2.30)两边取反拉氏变换,并令,则有

通常称h(t)为系统的冲击响应函数。

对于任意输入x(t)所引起的响应y(t),可利用两个函数的卷积关系,即响应y(t)等于脉冲响应函数h(t)与激励x(t)的卷积:

所以,冲击响应函数可以描述系统的动态特性。

传感器的种类和形式很多,它们一般可以简化为一阶或二阶系统。分析了一阶和二阶系统的动态特性,就可以对各种传感器的动态特性有基本了解。

研究动态特性可以从时域和频域两个方面采用瞬态响应法和频率响应法来分析。

2.传感器的频率响应

传感器对正弦输入信号的响应特性称为频率响应特性。频率响应法是从传感器的频率特性出发研究传感器的动态特性的。

(1)一阶传感器的频率响应

一阶传感器微分方程为

(www.xing528.com)

令τ=a1/a0(称为时间常数),Sn=b0/a0,灵敏度归一化之后可得

一阶传感器的频率响应特性曲线如图2.16所示。

图2.16　一阶传感器的频率响应特性曲线

当ωτ≪1时,有A(ω)≈1,Φ(ω)≈0,这表明传感器的输出与输入呈线性关系,且相位差很小,输出能比较真实地反映输入的变化。因此,减小τ可改善传感器的频率特性。

(2)二阶传感器的频率响应

二阶传感器的微分方程为

二阶传感器的幅频特性和相频特性曲线如图2.17所示。

从图2.17可看出,传感器的频率响应特性主要取决于传感器的固有频率和阻尼比。

当ξ＜1,ωn≫ω时:A(ω)≈1,幅频特性平直,输出与输入为线性关系;Φ(ω)很小,Φ(ω)与ω为线性关系。此时,系统的输出y(t)真实准确地再现输入x(t)的波形,这是测试设备应有的性能。

(3)频率响应特性指标

①频带

传感器增益保持在一定值内的频率范围,即对数幅频特性曲线上幅值衰减3dB时所对应的频率范围,称为传感器的频带或通频带,对应有上、下截止频率。

图2.17　二阶传感器的幅频特性和相频特性曲线

②时间常数τ

用时间常数τ来表征一阶传感器的动态特性,τ越小,频带越宽。

③固有频率ωn

二阶传感器的固有频率ωn表征了其动态特性。

3.传感器的瞬态响应

传感器的瞬态响应是时间响应。在研究传感器的动态特性时,有时需要从时域中对传感器的响应和过渡过程进行分析,这种分析方法称为时域分析法。传感器对所加激励信号的响应称为瞬态响应。常用激励信号函数有阶跃函数、斜坡函数、脉冲函数等。

下面以传感器的单位阶跃响应来评价传感器的动态性能指标。

(1)一阶传感器的单位阶跃响应

一阶传感器的传递函数为

(2)二阶传感器的单位阶跃响应

二阶传感器的传递函数为

传感器输出的拉氏变换为

二阶传感器的单位阶跃响应为

二阶传感器对阶跃信号的响应在很大程度上取决于阻尼比ξ和固有频率ωn。固有频率ωn由传感器主要结构参数所决定,ωn越高,传感器的响应越快。图2.18为二阶传感器的单位阶跃响应曲线。阻尼比ξ直接影响超调量和振荡次数。ξ=0为临界阻尼,超调量为100%,产生等幅振荡,达不到稳态。ξ＞1为过阻尼,无超调也无振荡,但达到稳态所需时间较长。ξ＜1为欠阻尼,衰减振荡,达到稳态值所需时间随ξ的减小而加长。ξ=1时响应时间最短。实际使用中常按稍欠阻尼调整,ξ取0.6～0.8为最好。

图2.18　二阶传感器的单位阶跃响应曲线

(3)瞬态响应特性指标

①时间常数τ

一阶传感器时间常数τ越小,响应速度越快。

②延时时间

延时时间指传感器输出达到稳态值的50%所需的时间。

③上升时间

上升时间指传感器输出达到稳态值的90%所需的时间。

④超调量

超调量指传感器输出超过稳态值的最大值。