调节回路的特性及选择方法

15.4.4.1 振荡性能

如图15-101所示，调节对象与调节共同组成了调节回路。调节器在干扰量z或额定值（控制量w）发生改变时参入到调节回路中。对此，调节器根据是发生了干扰还是控制量发生了变化的不同情况，其所起的作用也不相同。当发生干扰时，调节器出现坏的调节状态，而在一个控制量变化时，则出现好的调节状态。调节器对调节对象适应性好，如图15-102所示，则调节量X的振荡迅速变缓合。

好的调节特征：

1）过冲宽度x_m小（图15-102a）。

2）调节时间t_an短。

3）调节时间t_aus短。

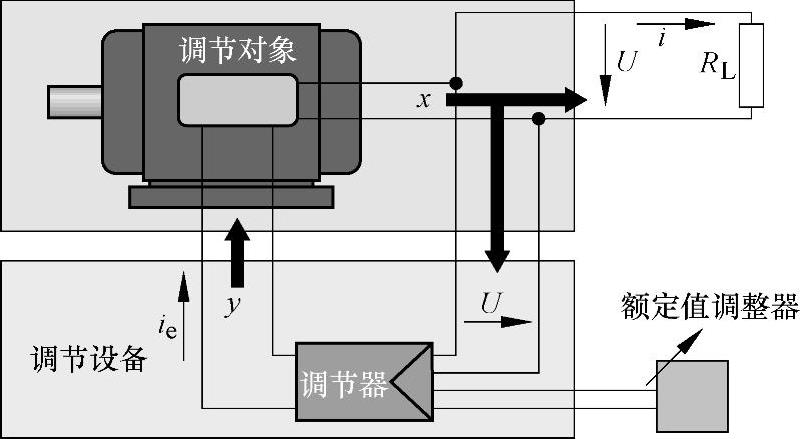
图15-101 调节回路

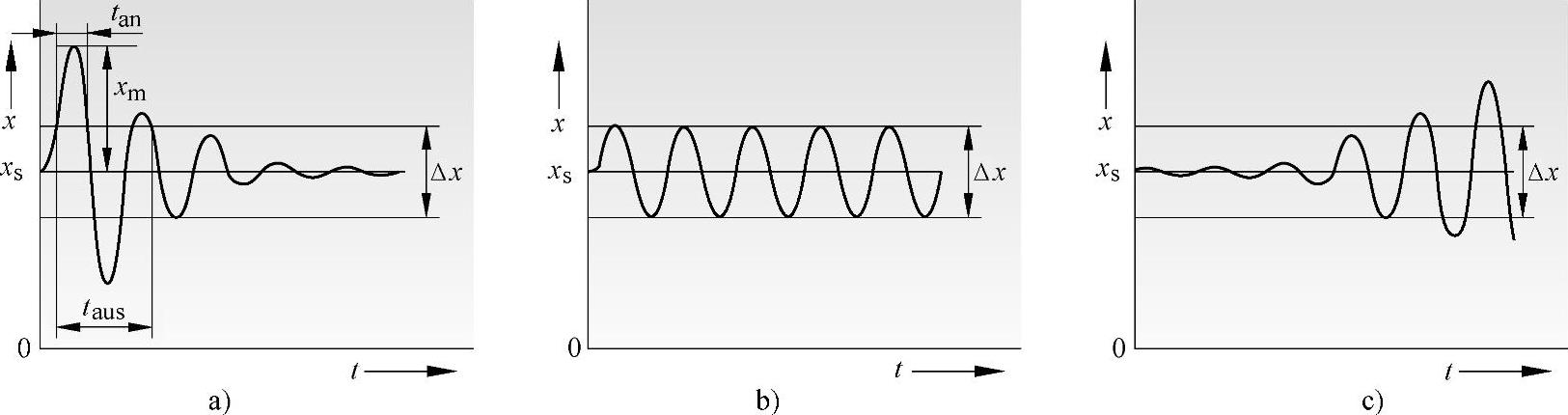
图15-102 调节回路特性

a）稳定的调节回路 b）调节回路处在稳定限度 c）不稳的调节回路 x_S—额定值 x_m—过冲宽度 t_an—调节时间 t_aus—调节时间 Δx—公差范围

•过冲宽度x_m：干扰开始后的第一个振幅。

•调节时间t_an：干扰开始与第一次达到公差范围Δx之间的持续时间。

•调节时间t_aus：干扰开始与调节量持久停留在公差范围Δx之间的持续时间。

没有调节系统的一般有约束力的质量标志，这与特殊的调节任务有关。对于一台车床的调节，因为许多零部件在转动，所以允许不给过冲，因此就可避免存在调节时间t_an和t_aus。

15.4.4.2 调节器选择

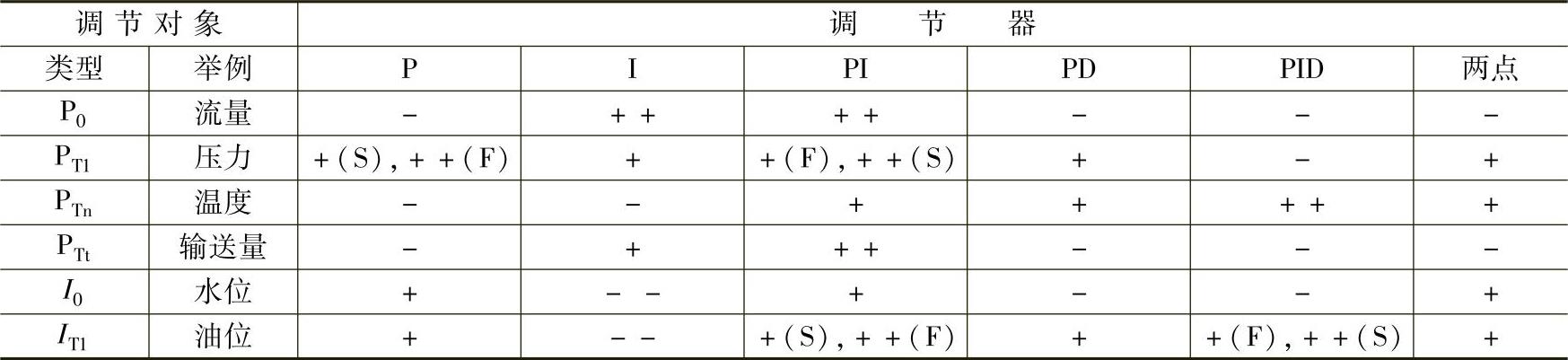
在建立一个调节回路时要规定调节对象。为了稳定而快速地达到控制，应选择合适的调节器（表15-14）。

表15-14 已知调节对象时调节器的选择

(www.xing528.com)

注：--—不稳定；-—不适合；+—适合；++—适合良；（F）—控制时；（S）—干扰时。

15.4.4.3 调节器的调整

如果所有的组成部分（调节对象、测量装置、控制装置及调节器）彼此相匹配，则调节回路便会稳定的工作。调节对象、测量装置与调整装置的性能是固定的并且多为已知的，因而只有调节器可以实现调整。一个可用的调节器调整证明是有困难的又是拖延时间的。对于熟练者是通过试验确定能得到良好调节效果的调节条件（表15-15）。

表15-15 调节器调整的方法

（1）按Chien/Hornes/Reswick法 使用表15-16中的方法的先决条件是调节对象的延迟时间T_u和平衡时间T_g已知。属于调节对象的还有控制装置和测量装置，因此必须要用控制装置和测量装置确定T_u和T_g。

表15-16 P_Tn调节对象按Chien/Hornes/Reswick法的调节器调整值

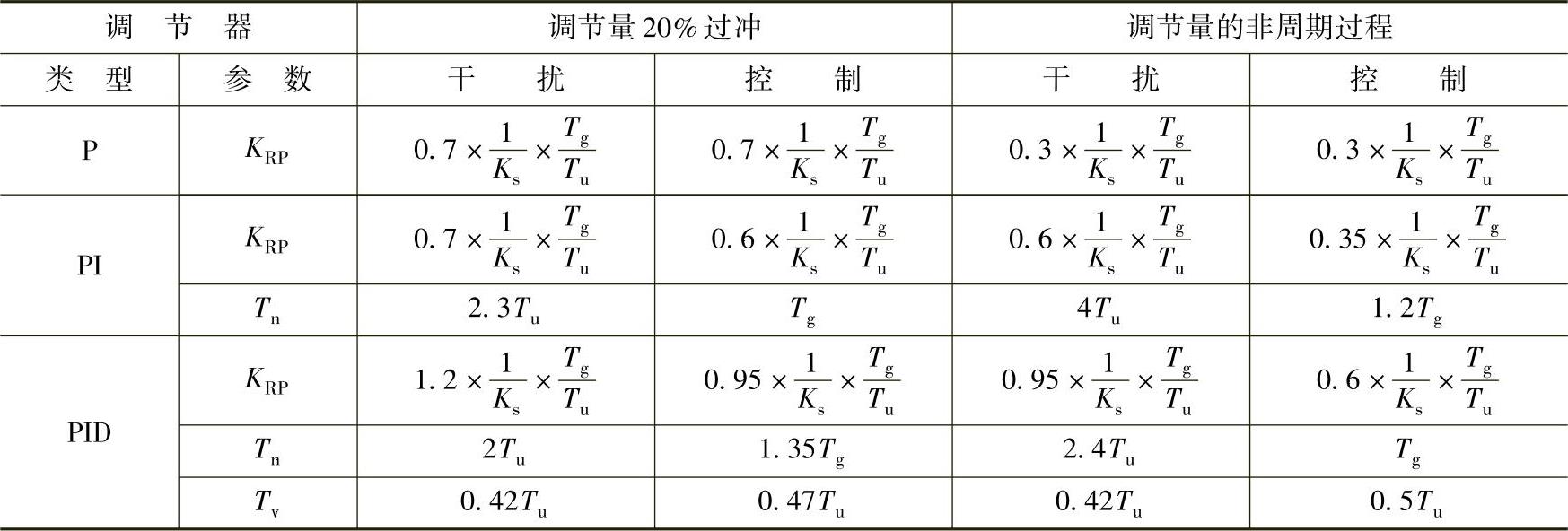
注：K_RP—调节器比例系数；K_s—调节对象比例系数；T_n—重调时间；T_v—提前时间；T_u—延迟时间；T_g—平衡时间有延迟时间的调节对象，在对于T_u的公式中脉冲实际延迟时间T_u使用延迟时间T_T；无平衡调节对象，在相应的公式中使用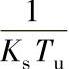代替。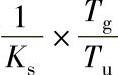

例题：

要对图15-103所示的退火炉进行调温。已知调节对象的延迟时间T_u=60s、平衡时间T_g=600s、比例系数K_s=10K/A。调节量允许有20%的过冲。请利用表15-16计算把干扰调整好的PID调节器的调整值K_PR、T_n和T_v。

解：

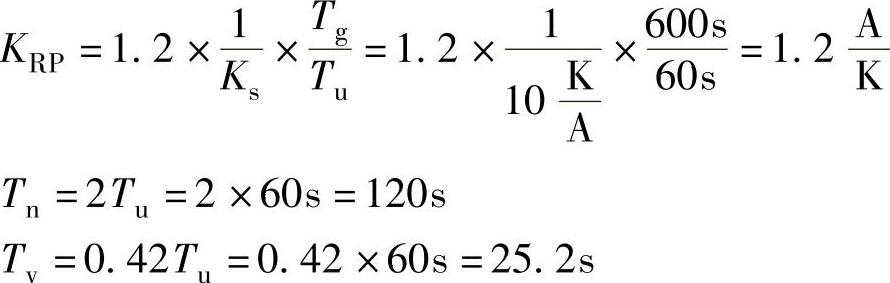
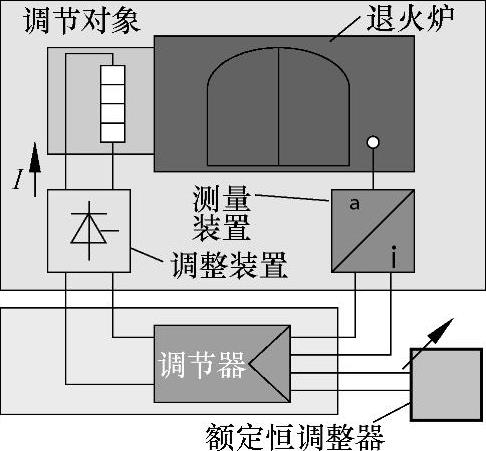
图15-103 退火炉的调温系统

（2）按Ziegler/Nichols法 当不知道调节对象的延迟时间T_u和平衡时间T_g时，则使用表15-17中的Ziegler/Nichols法。首先是作为一个纯P调节器（对于通用调节器把T_n调到∞，把T_v调到0），然后提高比例系数并直到调节量无衰减振荡为止。这种K_RP的调整称为临界比例系数K_RP0。然后测量调节量的无衰减振荡周期，此值是临界振荡周期T₀，为了获得调整值K_RP、T_n和T_v，则应按所选择的调节器把所发现的量乘以表15-17所列的值。

表15-17 按Ziegler/Nichols法的调节器调整值