运算法则。为了连接一个变量，如与图9-104所示的变量A连接，则在UND逻辑中或在有常量0和1的ODER逻辑中，以变量A本身或取反变量A，其运算定理是确定的，如图9-104所示。对于简化的逻辑等式，图中有红衬底一行的逻辑等式特别重要。
交换律指的是只包含有UND逻辑和仅包含有ODER逻辑的逻辑等式可以任意交换，而功能等式的结果不变（表9-41）。
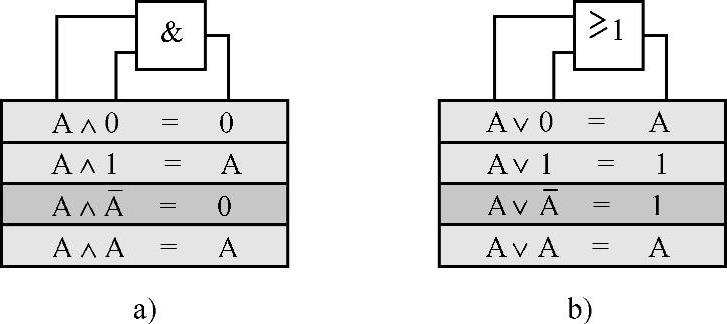
图9-104 运算法则
表9-41 布尔运算的运算规律
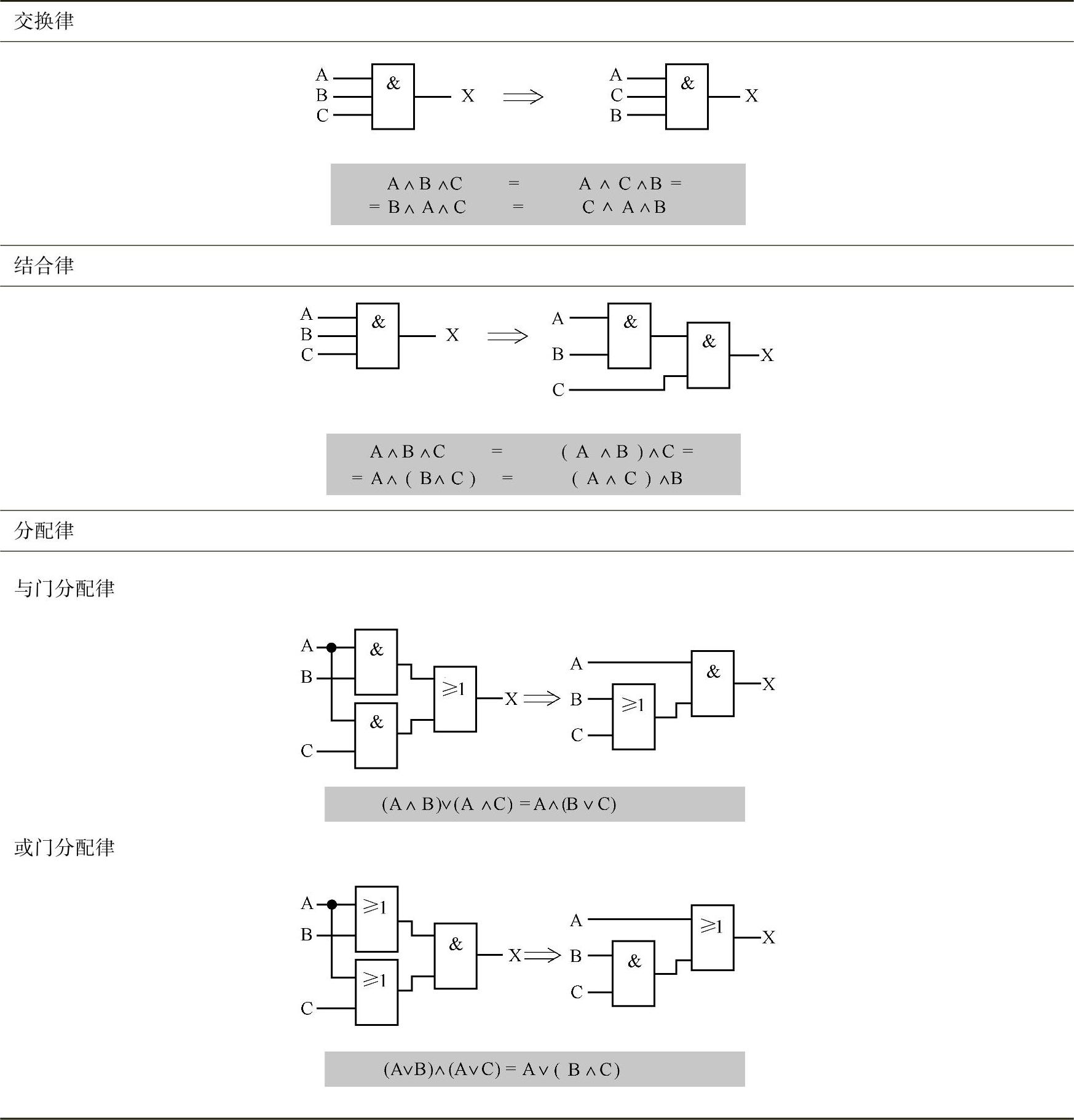
结合律表示在一个逻辑等式中把仅为一个逻辑类型放在括号中，但也可以省略。如果变量A、B和C在一个UND逻辑中处理，但只有一个组件可供使用，UND逻辑有两个输入，则可使用结合律（表9-41）。
分配律含有既包括有UND逻辑又包括有ODER逻辑的逻辑等式变换法则，在变换时应注意一个明确的写法，如括号的使用。
括号中的逻辑优先于未被括入括号的逻辑。
举例：
在X=A∧（B∨C）逻辑函数中，首先是变量B和C之间的ODER逻辑，然后把逻辑结果与变量A以UND逻辑处理。
在逻辑函数X=（A∧B）∨（A∧C）中，如果变量A和B或变量A和C有状态1（表9-41），则输出X有状态1。相同的功能通过一个以UND逻辑的分配律（与门分配律），获得变形的逻辑函数X=A∧（B∨C）（表9-41）。
按或门分配律把功能等式X=（A∨B）∧（A∨C）变化成相应的逻辑相同的电路X=A∨（B∧C）（表9-41）。
德·摩根定律（德·摩根，英国数字家，1806-1871）。利用德·摩根定律把UND逻辑转变为ODER逻辑（表9-42）。它主要用于减少所需要的开关电路的数量或用NAND组件或NOR组件建立一个电路。
表9-42 德·摩根定律
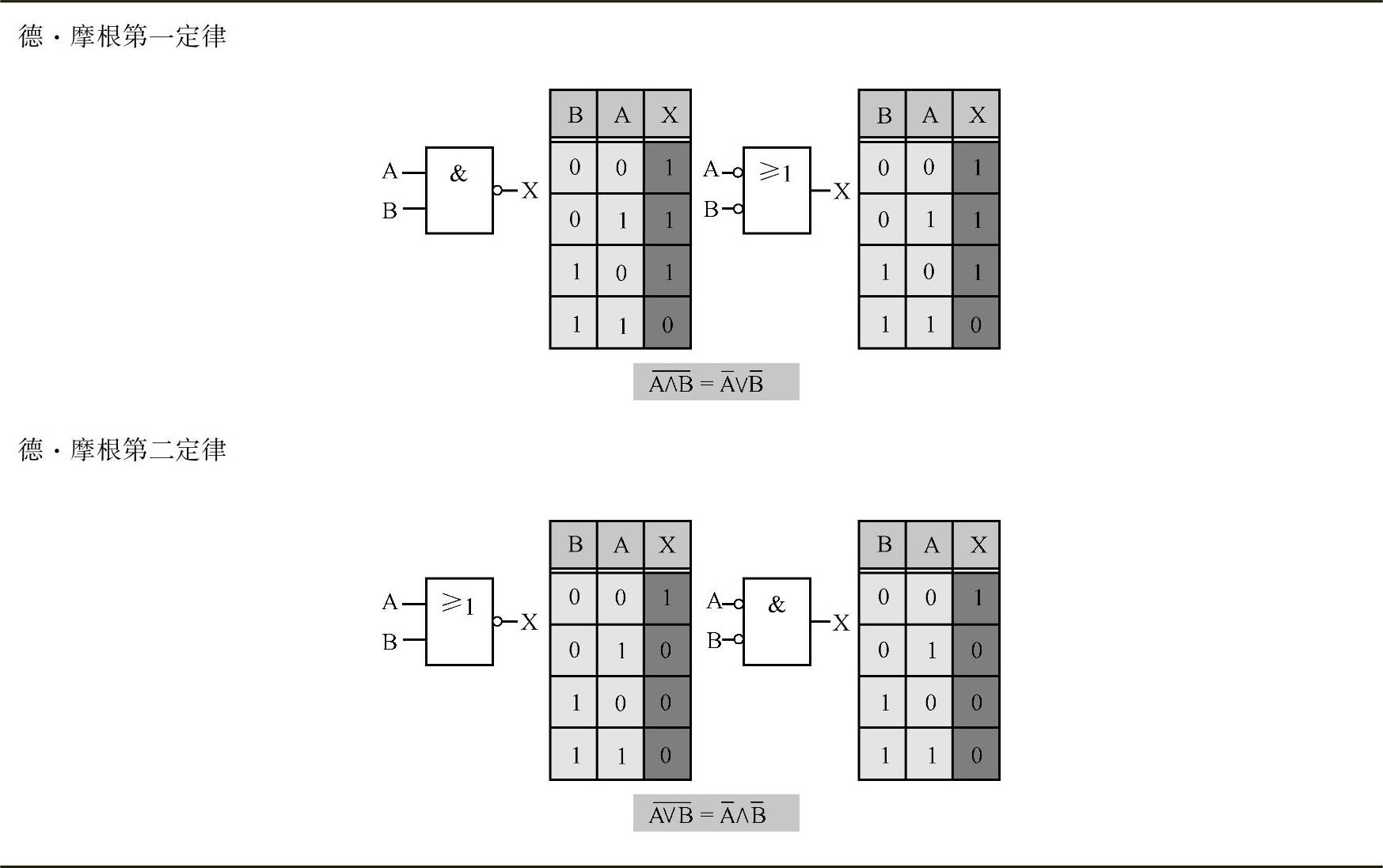
德·摩根第一定律是把一个NAND逻辑转换为具有取反输入的ODER逻辑。
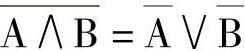
德·摩根第二定律是把一个NOR逻辑转换为具有取反输入的UND逻辑。(www.xing528.com)
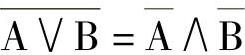
通过使用德·摩根定律可以把UND逻辑转变为功能相同的ODER逻辑及把ODER逻辑转变为UND逻辑，此时，逻辑的每个变量取反逻辑，且逻辑的运算符号发生变化。
两个连续逻辑的否定有：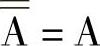
。
逻辑等式的化简
计算例题：
把图9-105所示的电路用逻辑运算定律进行化简。
首先从所给出的电路中取出全部部分逻辑（图9-105中的输入），并由此建立电路的逻辑函数。
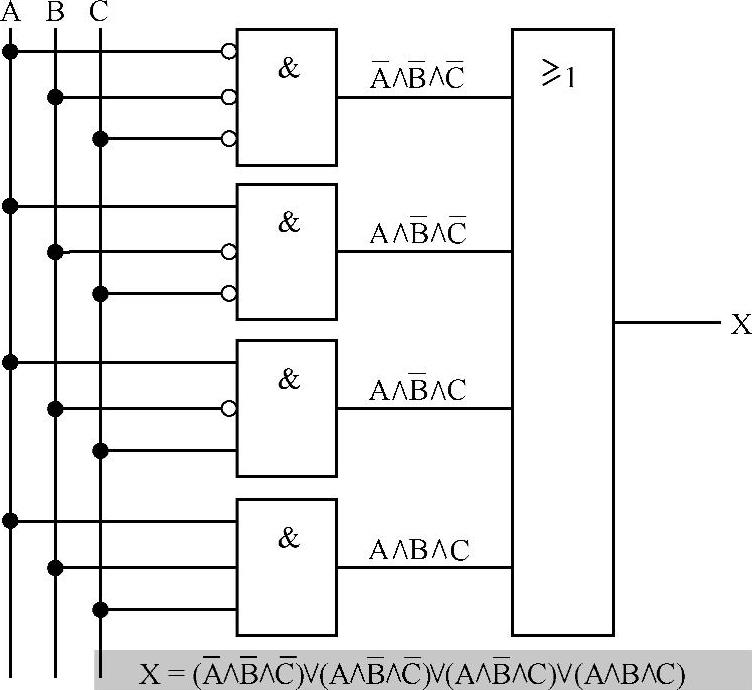
图9-105 电路举例
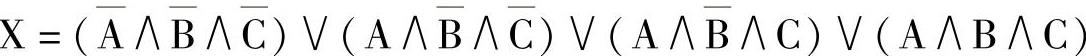
1）应用分配定律：
[从括号中取出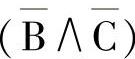
和（A∧C）]
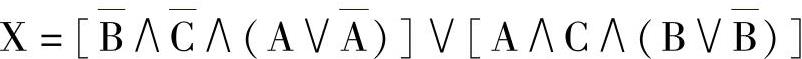
2）应用原则：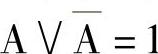
和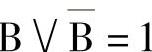
。
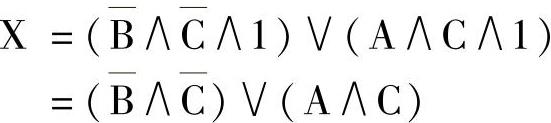
图9-106所示为化简了的电路。
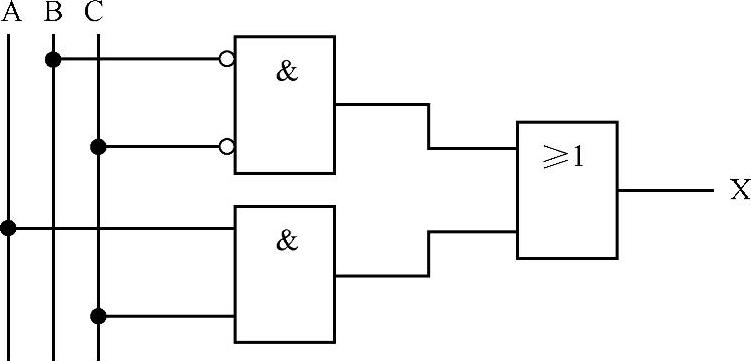
图9-106 化简后的电路
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
