三角形联结：如何使用符号△呈现？

电源，如发电机，其绕组为三角形联结。在三角形联结中只有3条线引向用电器，这样的电网称为三相三线制电网。380kV、220kV和110kV的高压电网为三相三线制电网。

在图7-81所示的三角形联结中，在每个相上都加有线电压。

图7-81 用电器的三角形联结（对称负载）

在三角形联结中，相电压等于线电压。

三角形联结的电压与电流：

式中 U——线电压；

U_Str——相电压；

I——线电流；

I_Str——相电流。

（1）对称（均匀）负载时的电流

实验7-27：把3个电阻为100Ω的相同用电器按图7-81所示以三角形联结接到一个交流变压器上，测量线电流和相电流。

线电流是相电流的倍。

在三角形联结中，线电流为分流（图7-81）。在利用节点原理时应注意单个电流相互是有相位差的，因此有一个几何总图。线电流I₁是I₁₂-I₃₁的几何差：I₂是I₂₃-I₁₂的几何差；I₃是I_31-I23的几何差。

在相电阻是有效电阻的电路中，如图7-82a所示，相电流I₁₂、I₃₁和I₂₃与所属的相电压U₁₂、U₃₁和U₂₃同相位。如图7-82b所示，为了确定线电流，允许平移相电流矢量，于是对于相电流I₁₂、I₃₁和I₂₃就形成一个星形。相电流之间的关系与线电流I₁、I₂和I₃一致。

在图7-82b，电流I₁₂、I₃₁和I₂₃构成一个基角为30°的等边三角形，此三角形可分为两个直角三角形，利用三角函数便得出：(www.xing528.com)

在三角形联结时，线电流I是相电流I_Str的倍。

计算例题：

在一个以三角形联结的三相用电器中，其每相的电流为2.5A。a）计算其线电流和b）画出其线电流（比例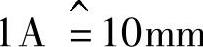：m）。

解：

a）

b）根据图7-82

解：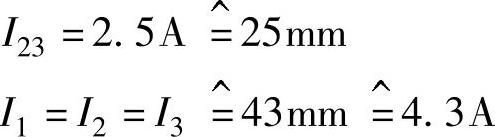

（2）非对称（不均匀）负载时的电流

实验7-28：用3个有效电阻重复实验7-27，但电阻值不同（图7-83a），计算其相电压、相电流和线电流，比较其相电压、相电流和线电流。

相电压相同，线电流不同，相电流也不同。线电流与相电流不存在的关系。

相电压的作用是在不同的电阻中流过不同大小的电流（图7-83b）。如实验7-28中有效电阻中的相电流分别为I₁₂、I₃₁和I₂₃，其相位与其各自所属的相电压U₁₂、U₃₁和U₂₃相同（图7-83b）。为了确定线电流，则平移相电流矢量（图7-83c），于是对于相电流I₁₂、I₃₁和I₂₃得出了一个非对称的矢量图。相电流之间的关系与线电流I₁、I₂和I₃相符。

图7-82 三角形联结的矢量图

图7-83 非对称负载三角形联结的电路与矢量图