把一个有效电阻R与一个电容器C串联后接到一个正弦电压上(图7-43a)。有效电阻上的有效电压Uw与电流I同相,而电容器上的电压滞后电流90°。在图7-43b所示的电压三角形中,容抗电压UbC矢量由电路电流I矢量向负方向(逆时针方向为正向)旋转90°后画出。
如图7-43b所示,总电流I超前总电压U,相位差φ是电流矢量与电压矢量之间的夹角。
图7-43c所示的电阻三角形和图7-43d所示的功率三角形可以通过电压三角得到,即把电压矢量除以或乘以总电流。这三个三角形为相似三角形。矢量三角形中的各个量可由勾股定理或三角函数计算得出。
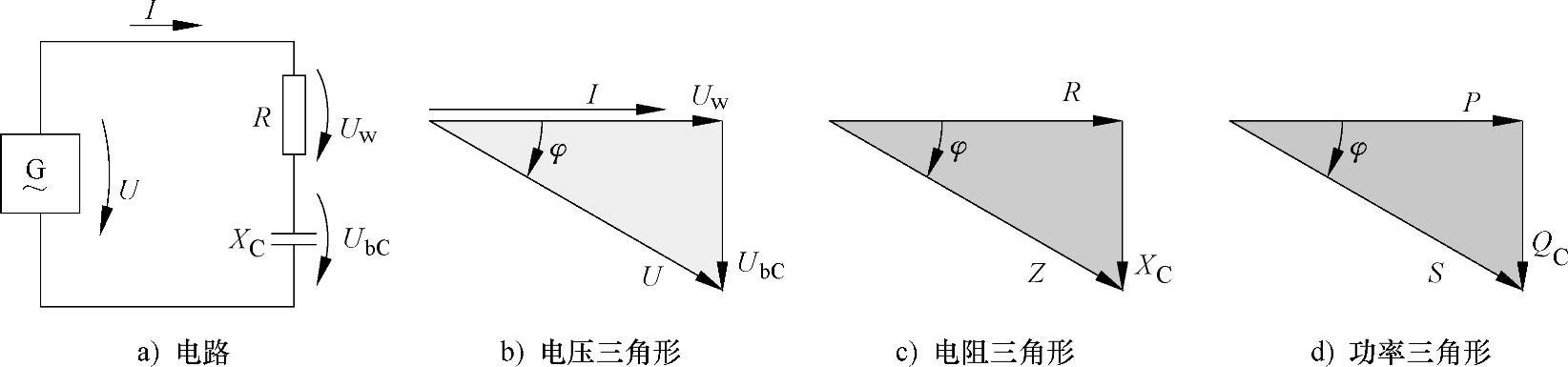
图7-43 有效电阻R与电容器C的串联电路
电容器与有效电阻的串联电路:
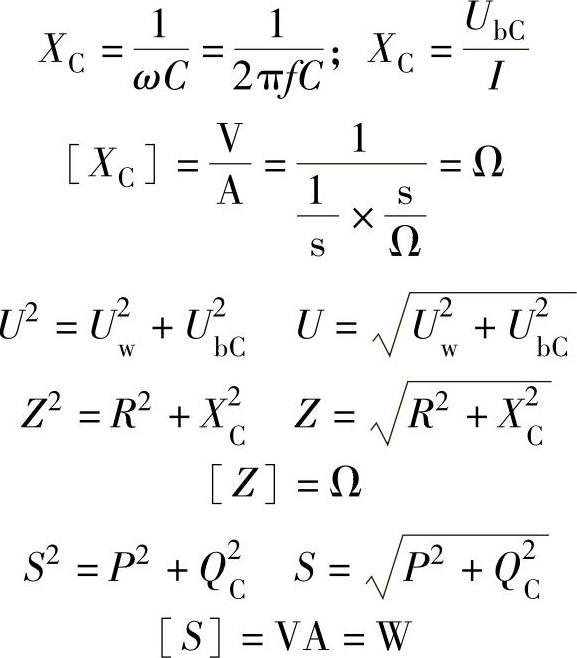
式中 XC——容抗;
UbC——电容器上的电压;
I——电流;
f——频率;
C——电容器的容量;
ω——角频率;
U——总电压;
Uw——有效电压;
Z——阻抗;
R——有效电阻;
S——视在功率;
P——有效功率;
QC——容抗功率。
计算例题:
把XC=35Ω的电容器串联到一个R=25Ω的有效电阻上,其串联电路的阻抗为多大?
解:
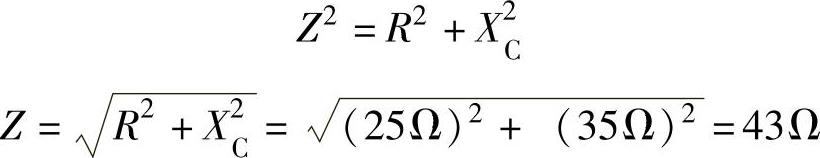
(1)RC高通滤波器 图7-44所示的RC电路称为RC高通滤波器。U1为输入电压,U2为输出电压。RC高通滤波器可以看是一个与频率有关的分压器,它将总电压U1分为UbC和U2两部分。在如f=50Hz的低频时,电容器C的容抗XC比有效电阻R大得多,因此R上的分电压很少;在为如f=10kHz的高频率时,电容器容抗XC比有效电阻R要少得多,这时的R上的分电压U2与电源电压U1接近。
在直流电源或如50Hz低频交流电作电源的电路中,如音频中央遥控制设备的控制信号的高频电压需要传输时,RC高通滤波器可用作输入或输出设备,其低频影响将被减少到最小程度。
(2)RC低通滤波器 图7-45所示的具有输入电压U1和输出电压U2的RC低通滤波器,也是一个与频率有关的电压分配器。在低频时,输入电压中的大部分加在电容器C上作为输出电压U2;在高频时,在电容器上只有很小的输出电压U2。
在具有高频的交流电压,如无线干扰电压需要抑制时,可用RC低通滤波器,以保低频电路不受影响。(https://www.xing528.com)
在使用RC高、低通滤波器时,输入电压往往是恒定的,但输出电压随频率而变化。不同频率的电压直角三角形可以在一个半圆中画出(泰勒斯圆,图7-46)。在极限频率fC时,电容器上的容抗电压等于电阻上的有效电压。
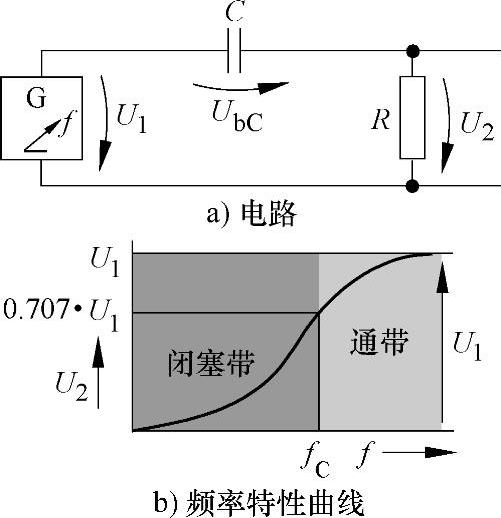
图7-44 交流电压与直流电压的隔断
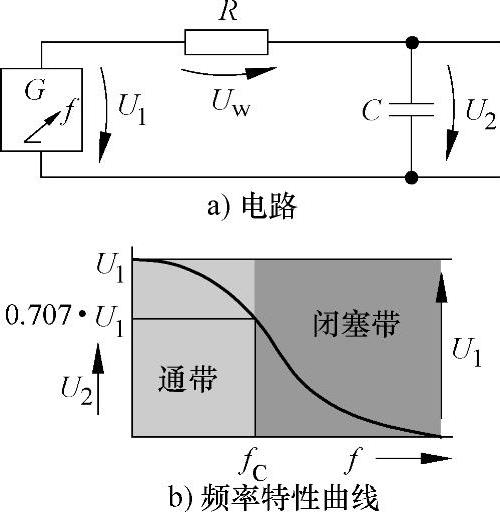
图7-45 RC低通滤波器
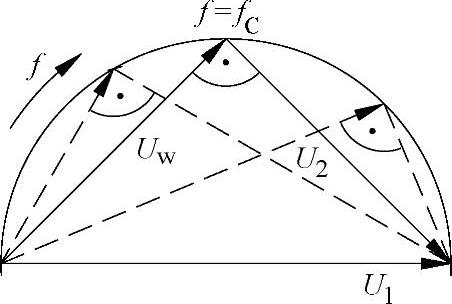
图7-46 RC低通滤波器电压三角形
在高、低通滤波器中,在极限频率fC时,有效电压等容抗电压。
由此关系可以计算极限频率fC时的输出电U2与输入电U1的比值。在串联电路中,在极限频率时RC高、低通滤波器的有效电阻R与容抗XC等值。
在已知有效电阻和电容器电容量的情况下,由以上关系可以计算出极限频率fC。
RC高、低通滤波器的极限频率
在极限频率fC有:
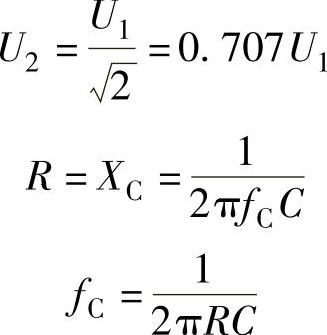
式中 U1——输入电压;
U2——输出电压;
fC——极限频率;
R——有效电阻;
C——电容量。
在一个放大器的电路中,通常可以用一个耦合电容器CK将混合电压U≃分离成直流电压U-和交流电压U~两部分(图7-47)。电容器容量的选择原则是:与有效电阻R相比,电容器容抗XC要较小,这样,电容器对于交流电压部分就不会产生阻碍。
交流电压U~的绝大部分降在电阻R上,只有极少的一部分降在电容器CK上,为了实现这个目的。因此,一般选择XC≈0.1R。
计算例题:
在放大器中,混合电压的频率f=50Hz,用一个耦合电容器CK分离出直流电压部分,使交流电压部分降在R=100Ω的电阻上,计算此耦合电容器CK的容量。
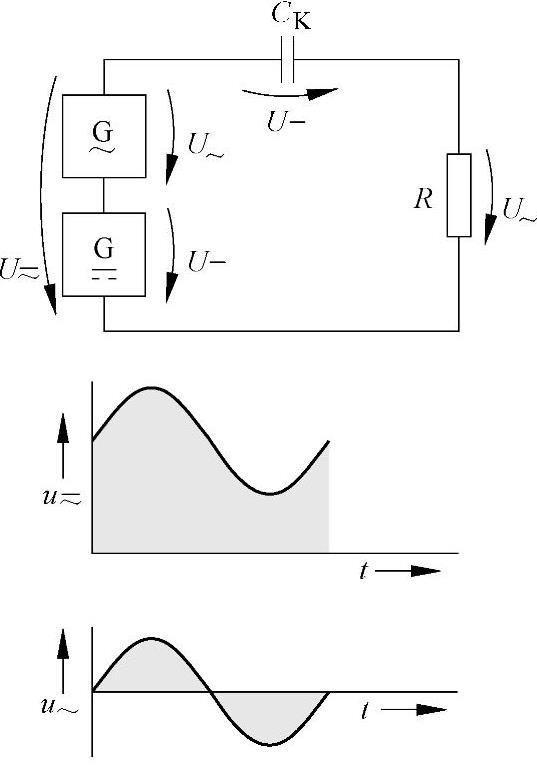
图7-47 直流电压与交流电压的分离
解:
选择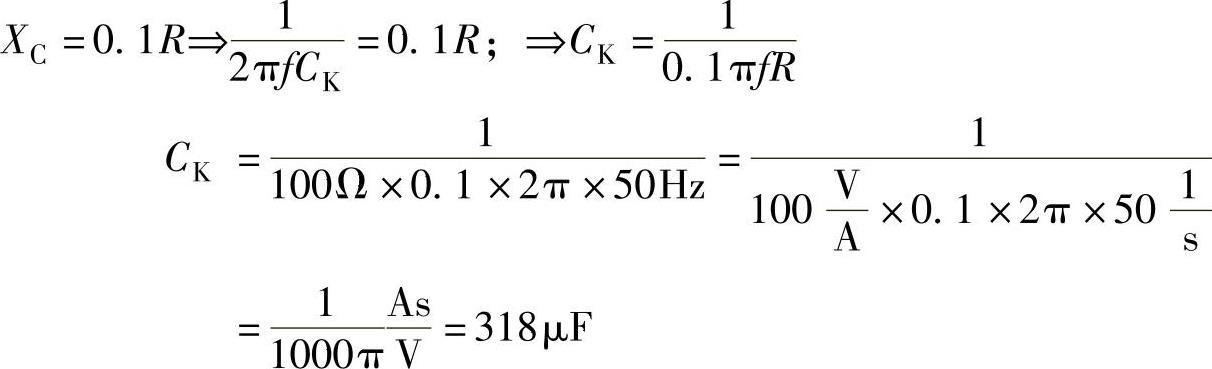
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




