串联电路中的阻抗三角形及其应用

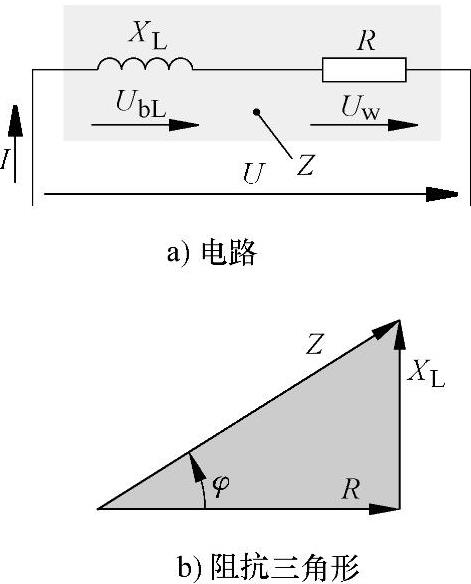
图7-26 阻抗

在图7-26a所示的电路中，若已知电阻上的电压降，便可以算出电阻值。串联电路中的阻抗Z可以通过阻抗三角形由勾股定理求得。由于R、X_L和Z上的电流是同一个电流，所以电阻与其相应的电压具有相同的比例，因此阻抗三角形与电压三角形相似。

串联电路中的阻抗：

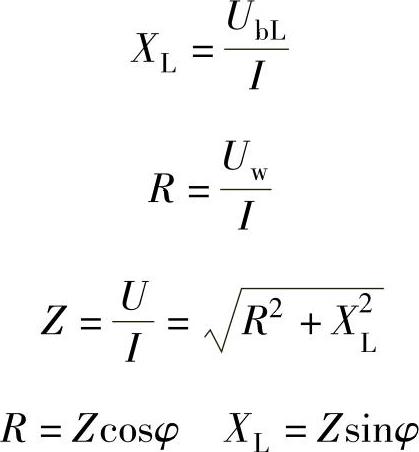
式中 X_L——感抗；

Z——阻抗；

U_bL——感抗电压；

U_w——有效电压；

I——总电流；

U——总电压；

φ——相位差。

计算例题：

由R=1kΩ的电阻和感抗X_L组成的串联电路在U=24V时的电流为I=4.8mA。计算：

a）阻抗Z。

b）感抗X_L。

c）电压U_w和U_bL。

解：

a）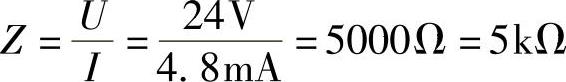

b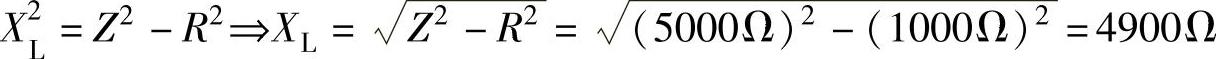）(www.xing528.com)

c）U_w=IR=4.8mA×1000Ω=4.8V

U_bL=IX_L=4.8mA×4900Ω=23.5V

实验7-11：将一个L=40mH的线圈与一个R=100Ω的电阻串联，接上一个如图7-27a所示的函数发生器的可变频正弦电压，把频率从50Hz调到5kHz，测量电压U₂。

随着电压频率的升高，电压U₂不断降低（图7-27b）。

RL低通滤波器。图7-27a所示的RL电路称为低通滤波器。RL低通滤波器实质上是一个与频率有关的把电压U分成U_bL和U₂的分压器。

在如50Hz的低频时，与负载电阻R相比，电感L有一个小的感抗X_L，所以电阻R上的电压为电源的大部分电压；频率升高后，如达到5kHz时，这时与负载电阻相比，电感L有大的感抗，于是，电源电压U₁的大部分施加到电感L上，而只有小部电压U₂施加在负载电阻上。

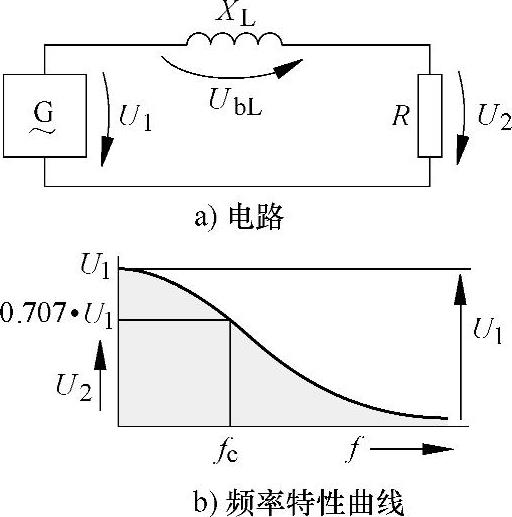
图7-27 RL低通滤波器

在极限频率f_c时，感抗X_L等于负载电阻R。

RL低通滤波器的极限频率，在极限频率f_c时有：

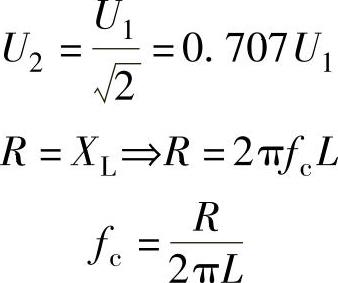
式中 R——有效电阻；

L——电感；

U₁——输入电压；

U₂——输出电压；

f_c——极限频率。

由此条件可以计算RL低通滤波器的极限频率f_c。在极限频率时，感抗电压等于负载电阻的电压降，因此可求得电压U₁与负载电压在极限频率时的比为。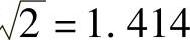

在电网频率如为50Hz的较低频率时，RL低通滤波器起通路作用；在频率较高时，例如干扰电压在回路中产生的电流，RL低通滤波器能将其抑制而起到滤波的作用。