实验7-9:把一个带闭合铁心的有3600匝的大电感量的扼流圈串联一个100Ω的有效电阻后接到频率为1Hz的正弦电压发生器上,用直流电压表和直流电流表(零点在刻度盘中部的指针式测量仪表)测量其电压和电流强度(图7-20)。
电流表指针的摆动比电压表指针滞后1/4左右的周期。
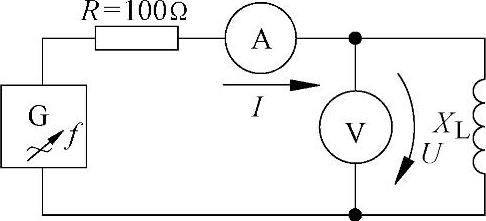
图7-20 实验:线圈中的相位差
对于实际的线圈,由于线圈中存在一个有效电阻,所以其电流与电压间总是有一个小于90°的相位差。
一个线圈可以等效为有效电阻与电感线圈的串联,并把此电路称为线圈的等效电路(图7-21)。
实验7-10:如图7-21所示,把一个有1000匝的线圈串联一个从零到1kΩ可调的电阻后接到一个函数发生器的可变频率的正弦电压上。调整可调电阻使电阻上的电压达到Uw=10V,并改变频率,使线圈上的电压为UbL=10V。测量总电压U。
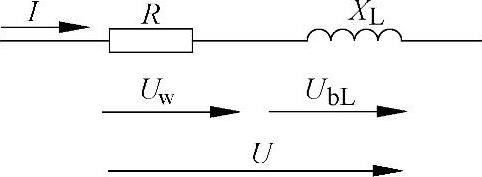
图7-21 线圈的等效电路
总电压U≈14V。
如图7-21所示,根据串联电路原理,在有效电阻R上有有效电压降Uw,在电感线圈XL上有感抗电压降UbL。实验7-10表明:因为有效电压与阻抗电压相差90°(图7-23a,图7-23c),所以两个电压的总电压不允许以算术相加来计算。
图7-22和图7-23表明了由有效电阻和电感线圈的串联电路的总电压和相位差的测定方法。
绘制具有有效电阻和感抗的交流电路矢量图的原则(图7-21和图7-22)。
①确定矢量长度的规定比例:如电压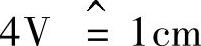 ,电流
,电流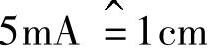 。
。
②以水平表示公共的原始值:在串联电路中的原始值为电流I。电流矢量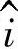 在X轴水平指向的右方。(https://www.xing528.com)
在X轴水平指向的右方。(https://www.xing528.com)
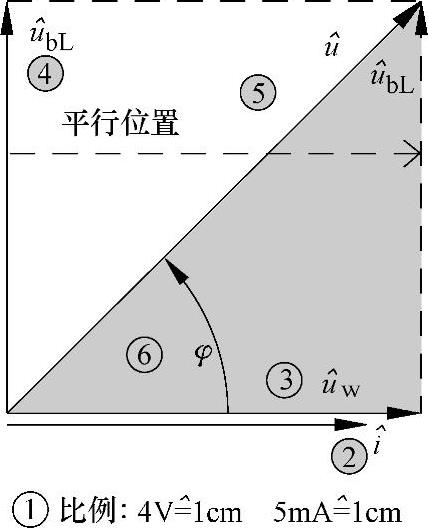
图7-22 电压的矢量图
③有效电阻R上的相位:
有效电压Uw和电流是同相位⇒电压矢量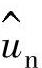 平行于电流矢量
平行于电流矢量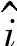 平放。
平放。
④电感线圈XL上的相位:
电感电压UbL超前电流I90°。⇒由于超90°,所以电压矢量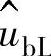 垂直于电流矢量
垂直于电流矢量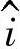 ,并指向上。
,并指向上。
⑤总电压是由通过相互结合的(矢量加)电压矢量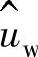 和
和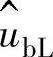 组成。矢量
组成。矢量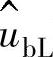 在矢量
在矢量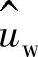 的峰值平行地右移,在所形成的矩形的对角线与总电压的幅值
的峰值平行地右移,在所形成的矩形的对角线与总电压的幅值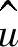 一致。
一致。
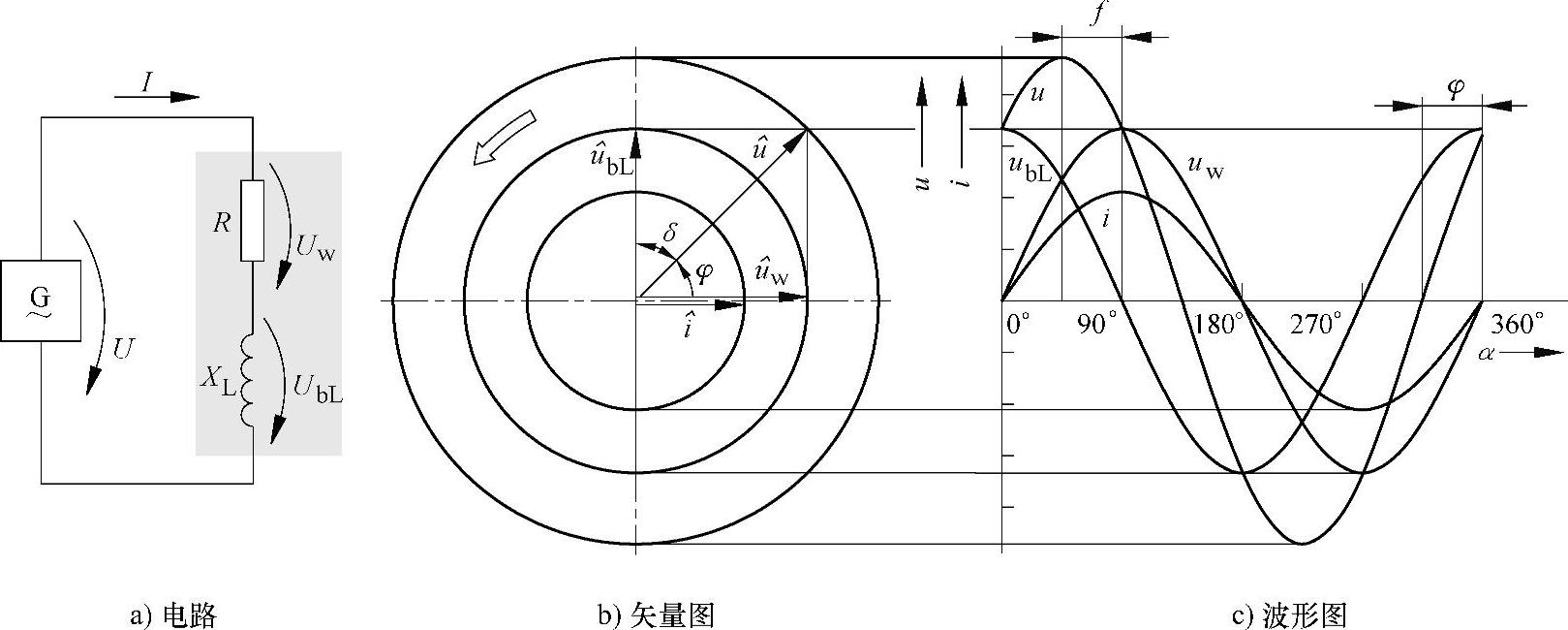
图7-23 有关电阻与电感组成的串联电路
⑥总电压u超前电流I,相位差φ是从电流矢量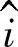 出发在电压矢量
出发在电压矢量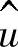 方向上来标注的。
方向上来标注的。
把电压和电流的最大值(幅值)除以系数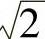 ,便得到了他们的有效值。所以,有效值的相量图与最大值的相量图相似(图7-24),由此得出:最大值
,便得到了他们的有效值。所以,有效值的相量图与最大值的相量图相似(图7-24),由此得出:最大值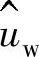 与
与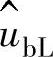 之间的相位差与有效值Uw和UbL间相位差相同,矢量Uw平行于电流I,电感电压UbL超前电流90°,总电压U是矢量Uw和UbL的矢量合(平行四边形法则)。
之间的相位差与有效值Uw和UbL间相位差相同,矢量Uw平行于电流I,电感电压UbL超前电流90°,总电压U是矢量Uw和UbL的矢量合(平行四边形法则)。
有相位差的正弦量的有效值必须是矢量合。
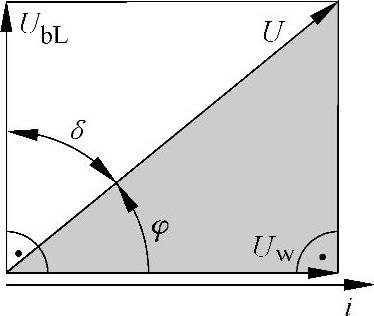
图7-24 矢量的相加
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




