局域网连接下的车库子系统模型：任务分配、车库数据库管理及设备干预

前已说明，液压大系统模块式建模法的数学模型是通过已标准化的子系统或子元件系统的数学模型简单地组装在一起的。因此我们先将子系统的数学模型的形成加以阐述。

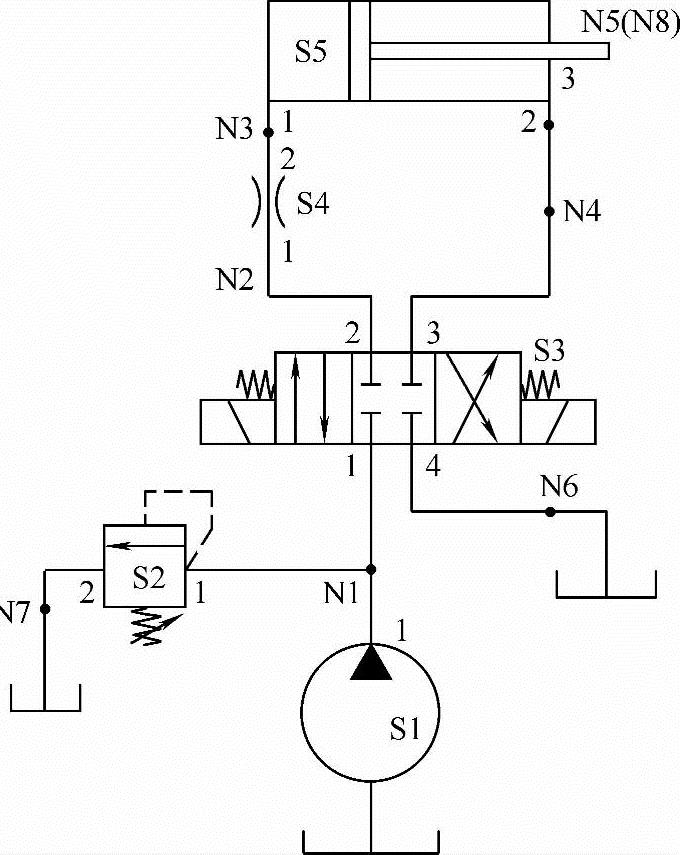
图6-3 建立子系统模型的液压调速系统

现利用我国秦川机床厂生产的QCS0003调速系统教学试验台的液压调速系统为典型范例（图6-3），来说明液压模块式建模法的子系统模型的形成与有关规则。为了便于说明问题，我们避开一些在建模过程中的细节与技术处理，以说明概念为准。我们规定在任何液压系统中所组成此系统的元件就成为此系统的子系统。在此液压调速系统中有5个元件，即有5个子系统。

1.子系统的“拓扑特征值”

所谓子系统的拓扑特征值即是描述此子系统特征的编号规则。它包括四个：

子系统（元件）辨识值C（特征编号值）；子系统（元件）序列值M（系统序列编号）。

子系统的接口编号N；子系统接口在系统中的结点编号J。

在此液压调速系统中子系统的拓扑特征值如表6-1所示。

表6-1 液压调速系统的拓扑特征值

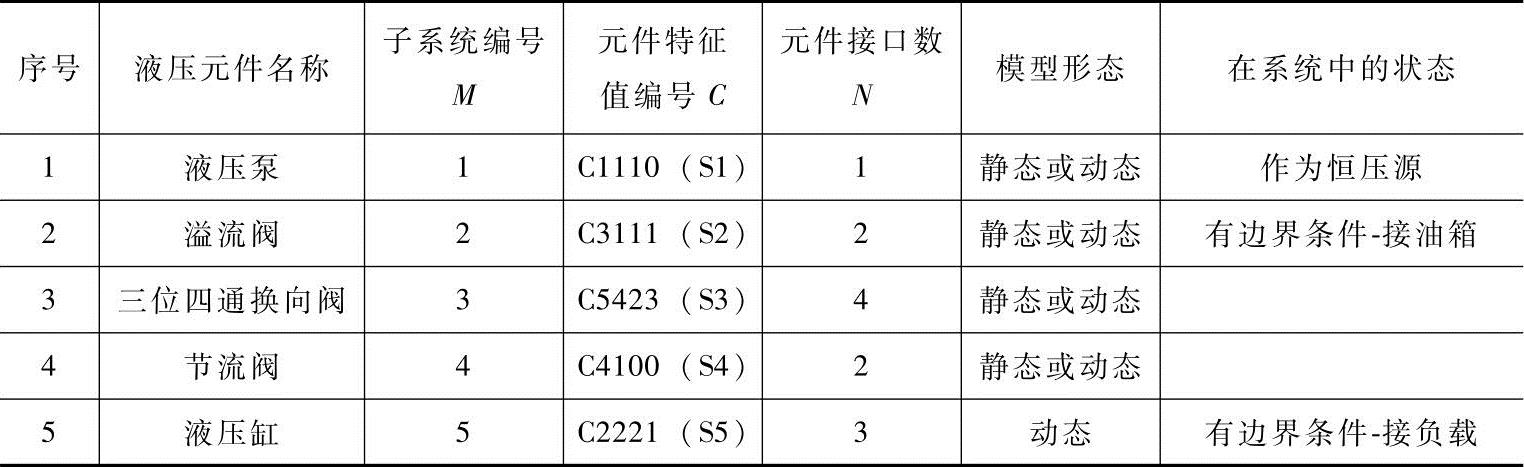
在表6-1中的模型形态是指子系统模型可以只用静态形式，此时模型方程中的导数项设为零。系统或子系统函数具有导数项是为动态方程。

2.相应的子系统模型

针对每个子系统的接口写出其相应的流量方程或力方程。对于有n个接口的元件就应该有n个流量方程。

由表6-2可见，该系统的元件作为子系统都可以按其连接口的流量（力）公式作为其子系统的数学模型。为此，有下列的液压子系统建模通用规则：

液压子系统模型必须写成是流函数U为左函数，而势函数V一般为独立的状态变量，是右函数。其函数一般表达形式为式（6-3），即为，。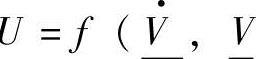

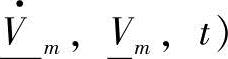在具体液压系统模型中，流函数用U表达，一般代表的是流量q、速度v等；势函数用V表达，一般代表的是压力p、力F等。必要时作为函数运算时要设置中间变量V_m，此中间变量主要是对于高阶的变量在函数运算时设置，也就是说，对于高阶函数可以通过中间变量低阶化到一阶。对用户来说一般无需顾及，在仿真中由程序自行处理。

系统阶次在液压系统中可以考虑不超过三阶。一则是此子系统根据硬件功能进行分解细化，或则采用一般降阶原则设置中间变量处理。

在上例中，对于液压缸是二阶微分方程，其降阶可设置中间变量为x。则需要增加一个降阶方程：由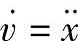降阶为

如果子系统模型内出现流函数的一阶导数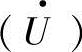也是允许的。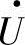函数实际是反映了子系统的液感，即流量变化对压力造成的影响。在仿真程序中必须顾及此运算，这样会极大地增加软件程序的运算量。

1）模块式建模法以状态空间法为基础，即在时域基础上考察系统的行为。对于子系统以其进出口的性能参数作为状态变量，对于系统则以子系统联接以后的结点处为状态变量，子系统的状态变量与系统的状态变量实质上是完全一致的。故此法称为性能参数建模法，又由于系统的模型是由独立巨标准的子系统模型经一定规则组装而成，故此法又称为模块式建模法（后一名称更易理解及突出此法形式上的特点，故此法定名为模块式建模法）。

2）以子系统的进出口性能参数作为状态变量，可以保证这些变量的可测量性及可观察性。

3）状态变量分为相等型变量（如p，v等）及相加型变量（如q，F等）两大类，亦或称相等型变量为势变量（以E或V表示），相加型变量为流变量（以F或U表示），这与键合图中对势变量E或力变量与流变量F的定义有差异。

表6-2 液压调速系统的子系统数学模型(www.xing528.com)

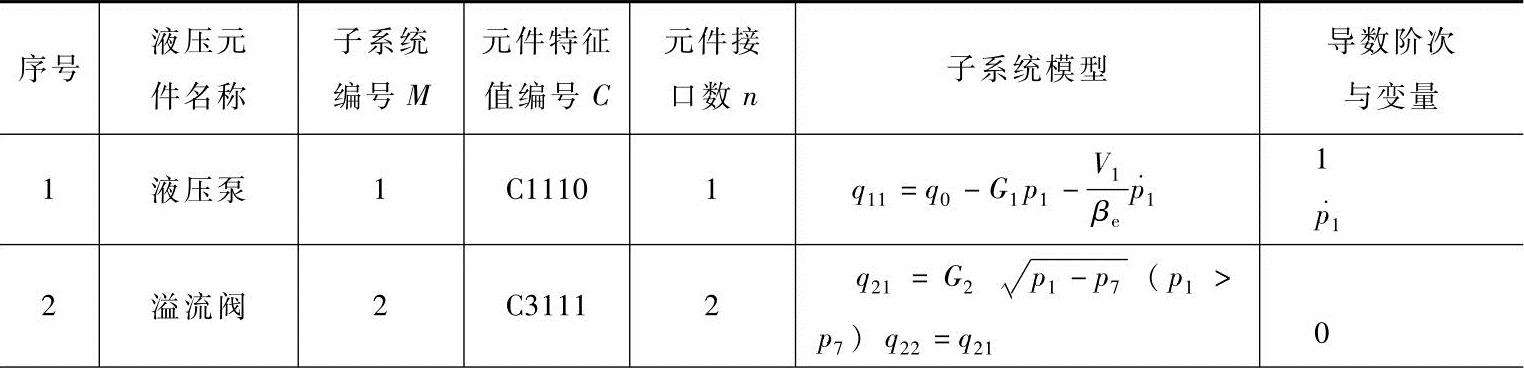
（续）

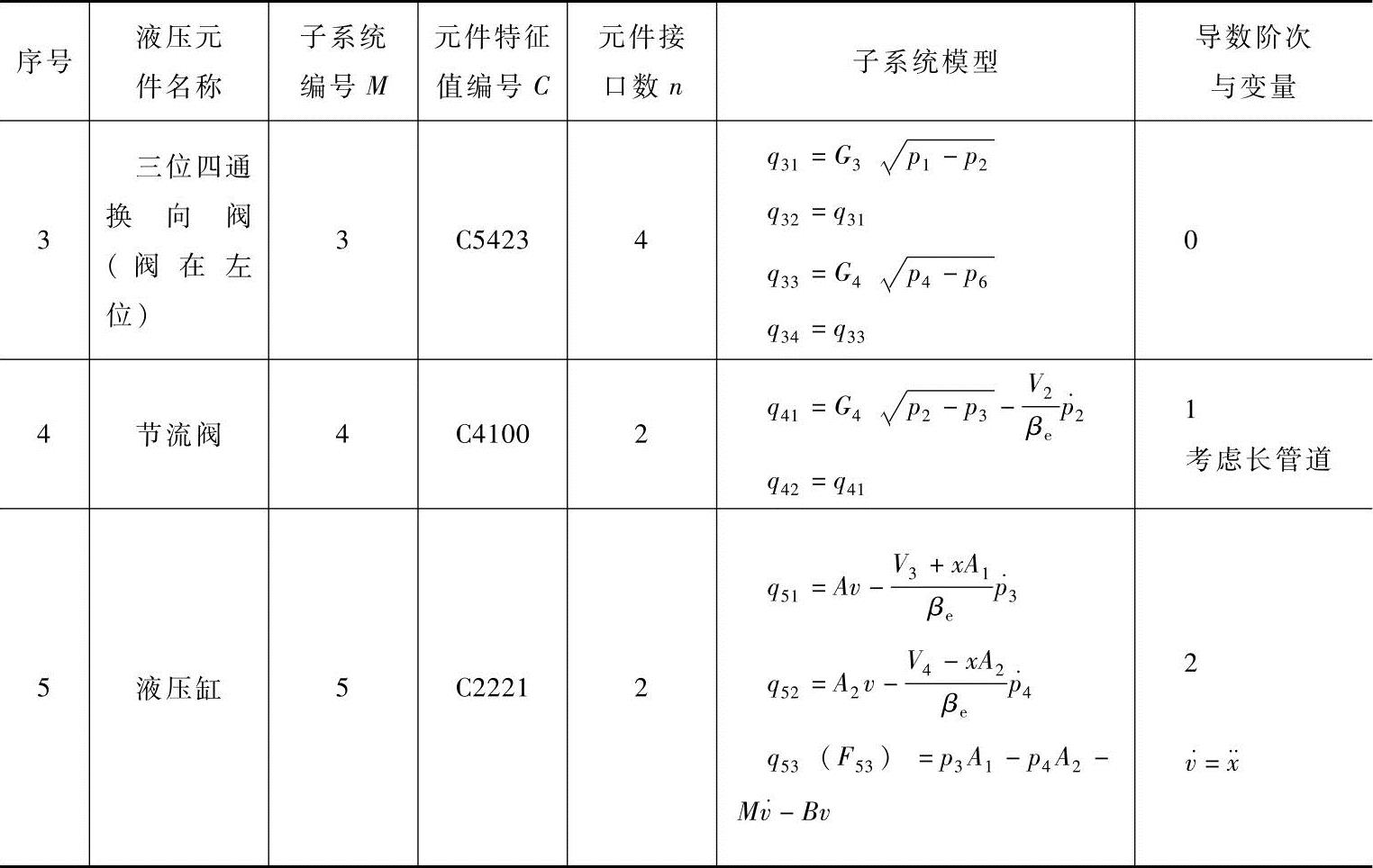
表6-2中符号意义如下：

4）子系统的数学模型是以势变量为独立变量的，子系统状态空间则由能量进出口的势变量进行描述，因而任何子系统具有能量交换口的数目与该子系统的状态变量数目一致。

5）非能量交换口如信号口处的变量不设立，信号（包括反馈）单独处理。

6）子系统的数学模型一般表达式是以势变量V为自变量，流变量U为因变量的方程。此数学模型一般可表达为：

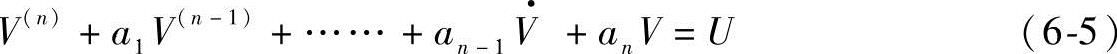
此时，若已知V^（n-1）（0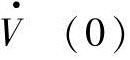），…，，V（0）和t≥0时输人，子系统的未来行为可以完全确定。

7）在划分子系统时一般以物理模型的明显界限区分，如液压系统中的子系统即是组成此系统的元件，液压元件作为系统时其子系统即是组成此元件的功能部件。

8）液压子系统与子元件数学模型的最高阶次一般为二至三阶，若过分追求模型的细化有时阶次会达到很高，例如四阶以上（如先导式溢流阀），经仿真与实验证明，这是没有必要的，模块式建模法中子系统模型的降价处理是合理的。

9）降阶处理的原则是：简化物理模型，或将物理模型进一步细化，这样可以做到子系统模型阶次不超过二至三阶，这时可设置中间变量形成一阶常系数微分方程。

10）在简化物理模型时可能产生非系统状态变量的中间变量，此变量用V_m来表示。

11）子系统的状态方程可写成式（6-6），此形式与系统状态方程相一致：

这里，f控制规律适于整个V（t）的函数范围，对液压系统而言，无论是伺服控制系统或传动系统（前者连续，后者常为不连续控制系统）均合适。

12）在处理子系统元件模型时，原则上与子系统模型的处理无区别，然而由于子元件更简单，因而其模型阶次的问题较简单，一般不超过二阶，但其系统矩阵中数量级比子系统小，在运算上更易产生刚性问题。

13）子系统或子元件的数学模型本身也可作为一个系统或元件的数学模型，只要输人相应的边界条件即可。

14）子系统或子元件数学模型中的方程形式已在表6-2液压调速系统的子系统数学模型中列出。其中负值表示该流量是背离或流出结点，正值为流人结点，也就是说规定流人结点的流量为正，流出时为负。

15）研究证明，按模块式建模法可对所有液压系统与元件列出所要求的模型形式（本书略）。

16）子系统（子元件）的数学模型可以分为静态模型与动态模型，这可以根据用户的要求选择，所谓静态模型是指数学模型中导数项为零时的模型。

17）子模型在建立时可以加强细化程度，在使用时可以由用户自行选择。选择的方式是赋予某些系数为零或一具体值。

18）子系统（元件）数学模型可分为自调型与外控型两种。自调型是指其性能仅仅取决于本子系统的内部参数与变量，而外控型的性能一定有外来参数或性能的影响例，如具有反馈功能的元件就一定是外控型。