控制器稳定性分析及参数设计优化

1.输出滤波器参数设计

LVRT－DVR每相H桥逆变器输出侧采用耦合电抗器Lf与耦合电容Cf串联方式构成滤波器，如图5－42所示，其中Rf为阻尼电阻。输出滤波器主要用于滤除LVRT－DVR输出补偿电压中的谐波部分。

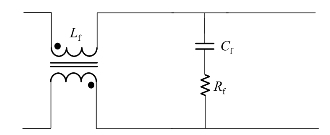
图5-42　LVRT-DVR输出滤波器

为保证逆变器输出电压中包含较小的开关频率成分，一般设计滤波器的截止频率远小于逆变器的开关频率，目的在于消除开关频率的谐波，即

一般情况下可以选择K≥5。

在保证滤波器滤波特性的前提下，电感值应当尽量小；一方面能减小逆变器的输出阻抗，提升对非线性负载的适应性；另一方面，电感值越小，逆变器越不容易发生超调的情况。电感量取小后带来的问题是电容必须增加，从而滤波器中高频电流成分也将大大增加。

设风电机组额定功率为750 kW，考虑1.2倍过载；单相额定电压为690 V，LVRT－DVR输出线电压最大有效值为1.0 p.u.，则单相最大输出电压有效值为

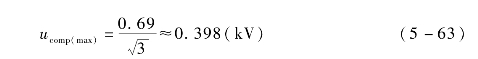
LVRT单相最大短时功率为

取IGBT的开关频率为3.2　kHz，通过PWM倍频，等效开关频率可以达到6.4　kHz，取电抗率为7.2%，则有

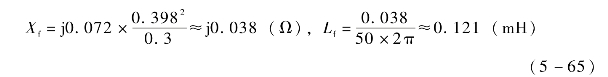
取K≈5，设定LC转折频率为1.2　kHz，则滤波电容的选择为

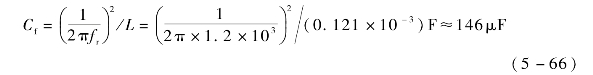
实际取140 μF，转折频率约1.22 kHz。

2.串联逆变器的闭环控制稳定性分析及控制参数优化

1）双闭环控制稳定性分析

由于实际装置使用数字控制系统，采样保持器对控制系统的影响应当予以考虑，其传递函数为

式中，T为一个采样周期，令s＝jω，则采样保持器频率特性为

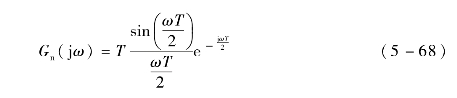
低频率下，采样保持器增益近似等于1，因此可将其近似为一个延时环节，即

对该延时环节做麦克劳伦展开，取其前四项：

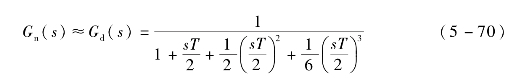(www.xing528.com)

将逆变器等效成增益为1的线性环节，结合状态方程即可得到系统状态空间模型，如图5－43所示，其中L、C分别为输出滤波电感和电容的取值。需要注意的是，这里虽然使用了三阶环节来近似因采样保持器造成的延时，但仍然会引入误差，尤其是对高频输入信号而言。

图5-43　系统状态空间模型

根据系统状态空间模型，可以得到前文所述输出电压瞬时值外环加滤波电容电流瞬时值内环反馈控制方法的系统框图，如图5－44所示，其中Ki1为电压外环比例系数，Ki2为电流内环比例系数。

图5-44　LVRT-DVR双闭环控制系统框图

根据双闭环控制系统框图，列出滤波电容电压uC（s）、参考电压uref（s）和系统电流io（s）之间的传递函数如下：

根据控制理论，分析式（5－71）分母根的取值即可确定系统的稳定性。现分析不同控制参数Ki1、Ki2下该系统根轨迹，以分析其稳定性。固定一个控制参数时，系统特征根对另外一个控制参数的根轨迹如图5－45所示。计算得T＝156.25 μs，L＝0.121 mH，C＝140 μF。

由图5－45（a）可知，随着Ki1取值的增大，某条系统特征根轨迹起点逐渐接近虚轴。当Ki1取值大于2时，该根轨迹完全位于正实部，系统无法稳定。因此，Ki1的取值应在0～2，此时通过Ki2的适当取值，系统能够保持稳定；图5－45（b）表明随着Ki2取值的增大，某条系统特征根轨迹起点先朝着远离虚轴的方向移动，取值超过一定范围后，又逐渐接近虚轴。当Ki2取值大于1.7时，该根轨迹完全位于正实部，系统无法稳定。因此，Ki2的取值应在0～1.7，此时通过Ki1的适当取值，系统能够保持稳定。

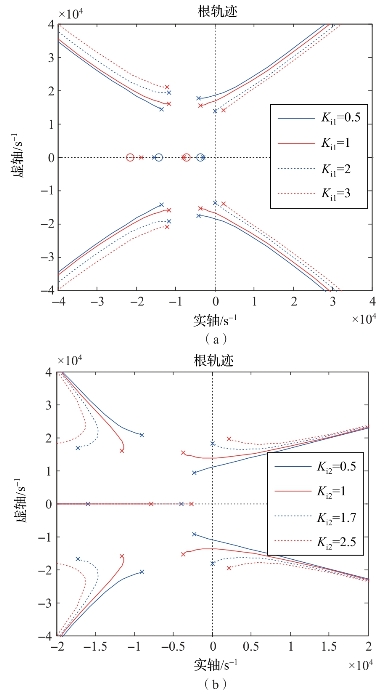
图5-45　系统的根轨迹图

（a）固定电压外环比例系数Ki1；（b）固定电流内环比例系数Ki2

2）双闭环控制系统及参数优化

对于LVRT－DVR而言，控制的目的主要在于使风电机组端口电压保持稳定，即滤波电容电压能够精确地跟踪参考电压，而风电机组输出电流对滤波电容电压的影响可视为一种扰动。上文通过根轨迹分析方法对该双闭环控制系统的校正参数Ki1与Ki2的取值范围进行了界定，下面通过选取不同控制参数，分析该控制系统的优化问题。

根据式（5－71）中滤波电容电压uC（s）与参考电压uref（s）的闭环传递函数，选取Ki1与Ki2允许范围内不同的参数组合，可以得到如图5－46所示的波特图。

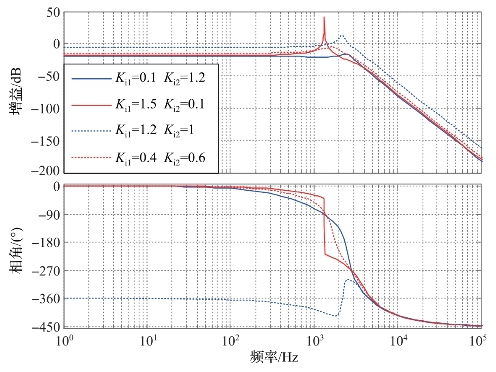
图5-46　双闭环控制系统uC（s）对uref（s）的频率响应波特图

为了使工频输出电压的误差较小，应使系统闭环传递函数在50 Hz附近的增益接近1（即0 dB）；同时，为了使逆变器输出电压谐波含量较低，系统在高频部分尤其是开关频率处的增益越小越好。通过对幅频曲线的观察可以看出，图5－46中所取的几组参数下，低频时闭环传递函数增益均小于1，该控制对参数的适应性较弱，可以考虑在控制环中增加前馈，从而提高控制系统对参数的适应性。图5－47所示为优化后LVRT－DVR双闭环控制系统框图。

图5-47　优化后LVRT-DVR双闭环控制系统框图

根据图5－47可得到滤波电容电压uC（s）与参考电压uref（s）的闭环传递函数，见式（5－72）。显然增加参考电压前馈后传递函数的分母部分没有变化，控制系统的稳定性不变，前文所界定的校正参数Ki1与Ki2的取值范围依然有效。

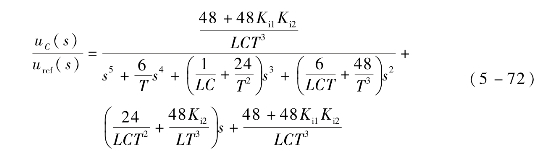
根据式（5－72）重新绘制波特图，如图5－48所示。图5－48表明，在50 Hz处，各组参数下系统增益对控制参数并不敏感，增益均接近1，控制系统对参数的适应性得到了大幅的增强，这主要是因为此时参考电压前馈对输出电压起主导作用；控制参数对系统性能的影响主要体现在系统的高频特性，不恰当的控制参数可能会造成逆变器输出谐波的放大。对图5－48的进一步分析表明，当控制参数取Ki1＝0.1，Ki2＝1.2时系统在高频段具有相对较好的滤波特性。

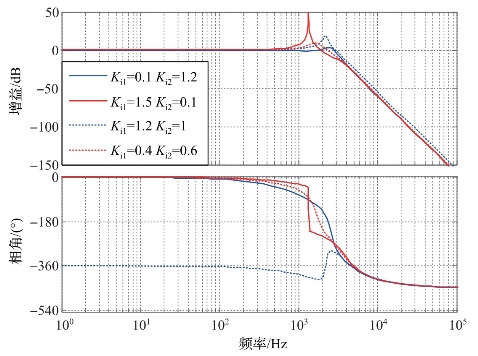
图5-48　优化后双闭环控制系统uC（s）对uref（s）的频率响应波特图