假设除与定子工频电流对应的频率为ω0-ωr的电流外,转子绕组中还存在一个频率为ω=ωSSO-ωr的交流扰动量Δir=Δird+jΔirq,在转子参考电流保持不变的情况下,RSC电压参考值的扰动量为
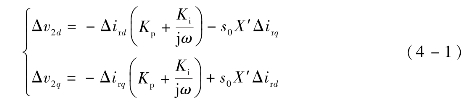
式中,Kp和Ki分别是RSC电流跟踪控制的比例系数和积分系数,s0=(ω0-ωr)/ω0是转子转速相对工频的滑差。
若RSC输出电压与其参考值完全相同,那么,RSC输出电压的扰动量为
![]()
双馈感应发电机的稳态等效电路如图4-29所示[22],图中vr是RSC的输出电压,s=(ωSSO-ωr)/ωSSO是转子转速相对定子扰动电流的滑差。
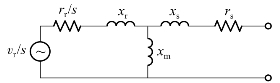
图4-29 双馈感应发电机的稳态等效电路
由前面的特征值分析结果可以看出,RSC控制参数对SSO的影响明显大于GSC控制参数的影响,因此,在分析SSO时,可暂时不考虑GSC部分的影响。根据式(4-2),在仅考虑扰动量的情况下,图4-29可重绘为图4-30(a)。利用阻抗代替其中RSC扰动量的等效电压源,可得到图4-30(b)。
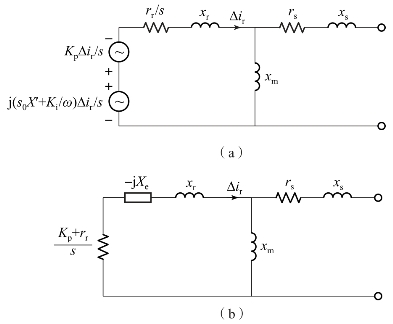
图4-30 仅考虑扰动量时DFIG的等效电路图
(a)含有电压源的等效电路;(b)电压源等效为无源元件
图4-30(b)中有阻抗
![]()
考虑到n台DFIG并联,对于准稳态的扰动量而言,风电场等值模型的等效电路如图4-31所示。

图4-31 扰动量下风电场等值模型的等效电路
当
![]()
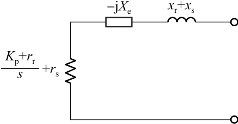
成立时,图4-30(b)中的励磁电抗xm可以忽略,进而得到扰动量下双馈发电机的近似等效电路,如图4-32所示。
 (https://www.xing528.com)
(https://www.xing528.com)
图4-32 扰动量下双馈发电机的近似等效电路
那么,图4-31所示等值模型的近似等效电路如图4-33所示。
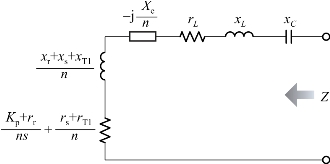
图4-33 等值模型的近似等效电路
对于频率ωSSO,定义整个系统的等效阻抗为

由于串补度小于100%,必然有ωSSO为次同步频率。若有X(ωSSO)≈0、R(ωSSO)<0,那么,在频率ωSSO上,该系统将会发生幅值发散的电气谐振,即SSO。
在传统的IGE现象中,整个系统的负阻尼由rr/s提供,显然,在大量安装双馈感应发电机的风电场发生SSO时,DFIG的变换器也参与了负阻尼的产生,其中,RSC电流跟踪比例系数Kp直接参与了等效负电阻的产生。
对于发生SSO的次同步频率,有滑差s<0,随着转子转速的提高,s的绝对值不断增大,使等效负电阻(Kp+rr)/s的绝对值不断减小,系统阻尼增强。所以发电机的转速越高,SSO对应特征值的实部就越小。伴随着系统阻尼特性的改变,谐振频率也会发生轻微的改变。
定义

显然,随着并网发电机台数n的增大,Le逐渐减小,谐振频率会随之升高。由于Le中存在n的倒数项,所以,DFIG台数越少,台数变化对Le的影响越大,对谐振频率的影响也就越大。根据式(4-5)可看出,随着n增大,等效负阻尼的绝对值减小,系统阻尼增加。随着n减小,谐振频率逐渐降低,励磁电抗ωSSO xm也会减小。当励磁电抗降低到一定程度后,就不能再忽略了。转子等效阻抗与较小的励磁电抗并联,使最终负电阻的绝对值减小,致使系统阻尼增强,这是SSO阻尼特性与并网发电机台数间非线性关系的原因。
根据图4-31可知,Kp与转子等效电阻直接相关,Kp越大,转子提供的负阻尼就越强,所以,Kp越大,SSO发散就越严重。为了使DFIG保持一定的响应速度,Kp不能太小,从而使得DFIG转子绕组在次同步振荡频率上的等效电阻较大,这是DFIG容易诱发IGE的根本原因。
随着线路电阻的增大,整个系统的等效电阻增大,系统的阻尼增强;随着串补容量的增加,系统的谐振频率会升高,同样转速下的滑差的绝对值会变小,使得等效负电阻的绝对值增大,因而整个系统的阻尼减小。
上述并网发电机台数、转速、RSC电流跟踪比例参数等对SSO特性的影响与前面特征值分析的结果非常一致,可见,图4-31所示的等效电路可以解释风电场SSO现象的一些基本规律,能够揭示SSO发生的机理。
在采用机端电压相量定向控制时,定子吸收的感性无功功率与定子次同步电流的q轴分量成正比。若只考虑控制环中的比例环节,定子无功功率的波动在RSC输出电压q轴分量上产生的波动为
![]()
式中,KpQ为无功功率控制的比例系数;vs为机端电压有效值;Δisq为定子扰动电流的q分量;Δirq为转子扰动电流的q分量。可见,对于q轴电流而言,转子等效电阻会增大,所以,KpQ越大,SSO发散越严重。
当转子中的次同步电流流过RSC时,必然会产生相应的电磁功率。该电磁功率会在直流电容上产生电压波动。由于直流电压比例控制的控制作用,GSC会输出相应的次同步电流以保持直流电压恒定。那么,GSC的直流电压控制环节就会改变DFIG输出的次同步电流,从而会对SSO产生影响。
另外,稳定的机端电压减小了发电机与输电线路间的电气耦合,削弱了串联电容对发电机的励磁效应。所以,增大GSC机端电压控制的比例系数能够增加系统对SSO的阻尼。
DFIG风电场SSO现象发生的机理与普通IGE现象的机理是非常相似的,不同的是在风电场发生SSO的过程中,DFIG的控制环节通过RSC和GSC向整个电气系统注入了额外的能量,改变了电气谐振的频率和发散速度。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




