风力机变桨距的数学模型

对于变桨距风力机，若只关心其向风电机组输出机械功率的特性，可以用捕获风能的稳态功率特性来建模，则风力机输出的机械功率Po可用式（2－1）表示：

从式（2－1）中可以看出机械功率Po不仅与风速v、空气密度ρ、风机叶片半径R有关，还与表征风力机风能转换能力的风能利用系数Cp有关，其物理意义是风力机输出机械功率与输入风力机叶片旋转面风能功率的比值。Cp是一个与桨距角β和叶尖速比λ有关的重要参数，λ的定义如式（2－2）所示：

式中，ωmech为风力机叶片旋转的角速度，与双馈电机转子电角速度ωr的关系可用式（2－3）表示：

式中，N为连接风力机和发电机的齿轮箱增速比。

Cp是研究风力机气动特性中最重要的一个参数，它代表了风速、转速以及桨距角等关键变量对一台结构参数确定的变桨距风力机捕获风能能力的影响，其经验公式可以用非线性的高阶函数式（2－4）表示［3］：(www.xing528.com)

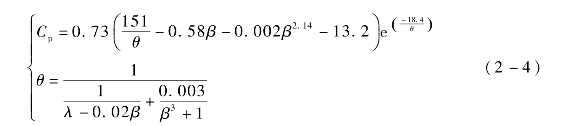
从式（2－4）可以看出，对桨距角控制的建模是研究变桨距风力机建模中不可缺少的一环。桨距角变化的执行器一般为电机或液压设备，其动态特性可以用一个一阶惯性环节等效，并且考虑到风力机桨叶的机械强度有限，桨距角的变化率也必须得到限制，则桨距角β的控制模型如图2－2所示。

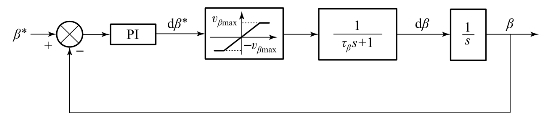
图2-2　桨距角β的控制模型

通过PI控制器作用产生的桨距角变化率的指令值dβ*，经过限幅环节作用后变化率的绝对值被限制不超过vβmax，再经过执行机构等效的一阶环节后得到变化率的实际值dβ，τβ代表一阶环节的惯性时间常数。最终的桨距角β由变化率dβ积分得到。

在得到桨距角的控制模型后就可以建立由风速v、风力机旋转角速度ωmech和桨距角β*计算变桨距风力机向发电机提供机械转矩TL的模型，如图2－3所示。图2－3中变桨距控制模型如图2－2所示，Cp模型为式（2－4）、Po模型为式　　（2－1）。

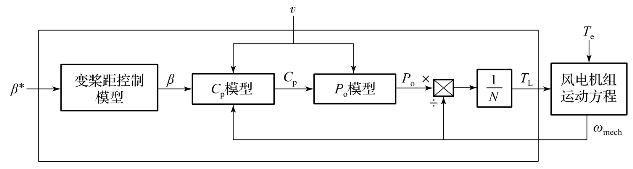
图2-3　风力机输出机械转矩的模型框图