电磁信号可以是模拟的,也可以是数字的。模拟信号的强度是不同的,信号强度的变化经常是平稳持续的。另一方面,数字信号强度在某个时期是一个定值,过一段时期它会变换到另一个离散的水平(Discrete Level)。图3-1表示的是模拟信号和数字信号。
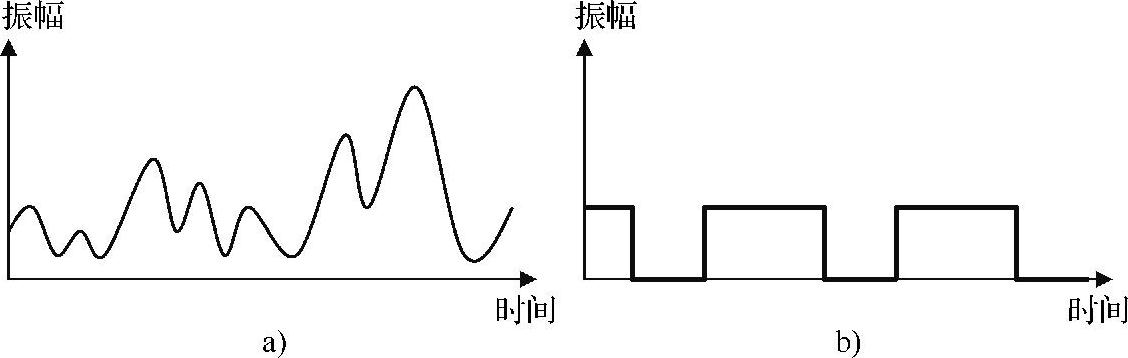
图3-1 模拟信号和数字信号
a)模拟信号 b)数字信号
当在某个时间周期之前的信号强度和某个时期T的信号强度相同,并且每个T内都重复,这种信号叫周期(Periodic)信号。图3-2表示的是代表模拟周期信号的正弦波和代表数字周期信号的矩形波,这里
s(t)=s(t-T) (3-1)
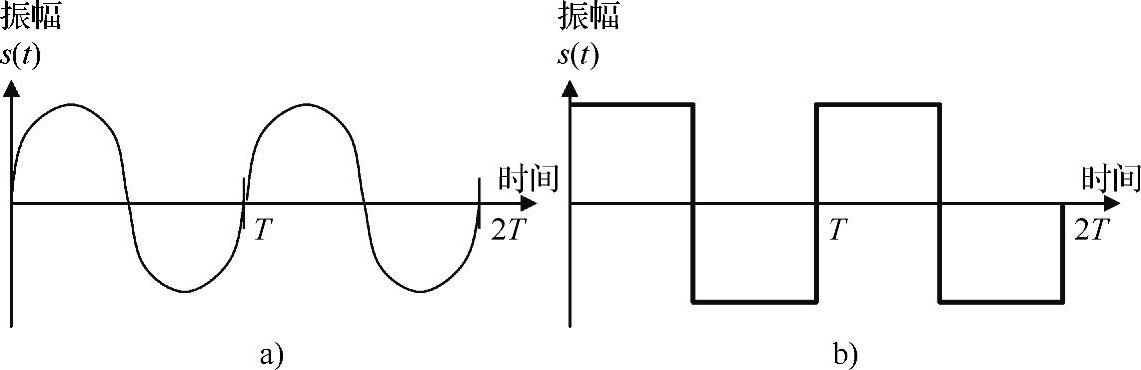
图3-2 正弦波和矩形波
a)正弦波 b)矩形波
周期信号的频率(f)是指每秒信号重复一个完整周期的速度,即f=1/T;这个速度是以赫兹为单位的(每秒的周期数)。例如,一个完整的正弦波是在每个T内完成2π循环,也就是360°,再开始一个新的周期。如果给出一个正弦波的峰值振幅A、频率f和初始相位ϕ,则时间t的信号强度是(https://www.xing528.com)
s(t)=Asin(2πft+ϕ) (3-2)
图3-2a的正弦波有一个单频率f,式(3-2)足以能表示正弦波为时间函数。不过,一个典型的电磁信号有不止一个单频率分量,因此电磁信号强度也需要表示成频率函数。例如,图3-3d的信号有三个频率分量。对三个频率来说,初始相位ϕ是0,表示起初正弦波的相位对所有的三个频率为0。图3-3a中第一个频率f的
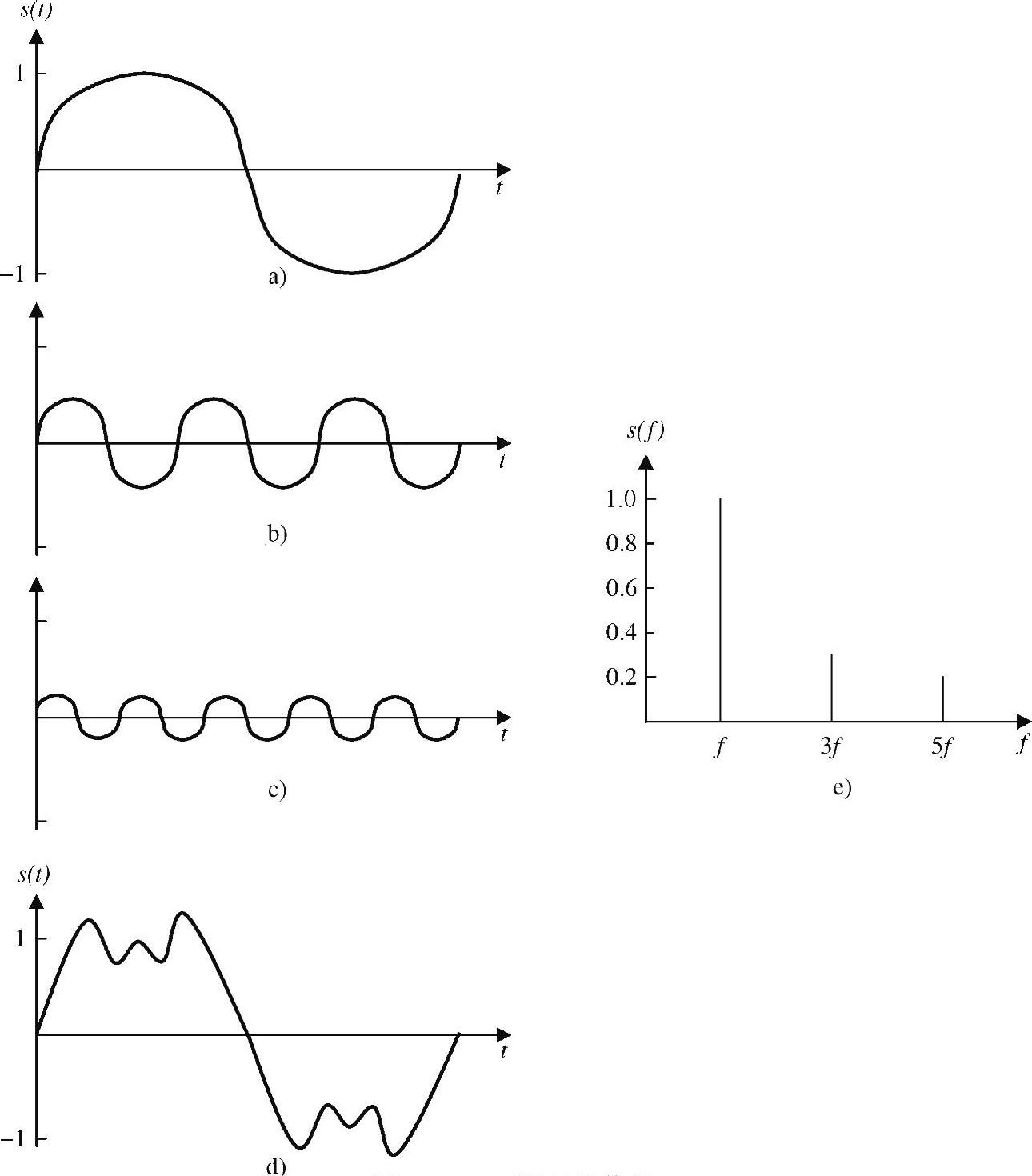
图3-3 4f带宽的信号
a)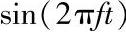 b)
b)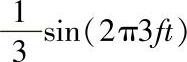 c)
c)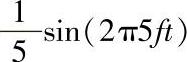 d)
d)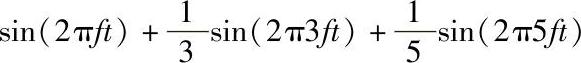 e)
e)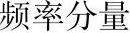
峰值振幅A是1。第二个频率是第一个的3倍,即3f,峰值振幅是其1/3,即A/3。第三个频率是5f,峰值振幅是A/5。这个信号涵盖了f~5f之间的频率,带宽为4f。例如,如果f是2MHz,这个信号的带宽为8MHz。
当把图3-3中频率为f、3f和5f的波形叠加在一起时,可以得到如图3-3d所示的波形。它看起来像数字矩形波。加在此信号的频率分量(Frequency Component)越多,它就越接近一个矩形波,失真也会越少。实际上,当有无数个频率分量时,它变成矩形波。换言之,矩形波有无穷个频率分量,可以把它表示成
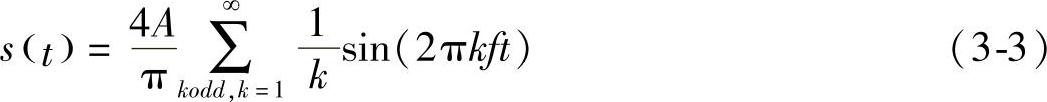
注意,随着每个额外频率分量的增加,它的峰值振幅会降低,比如kf的峰值振幅是A/k。因此,大部分能量是在最初的一些频率分量里。另外,每一个频率分量的衰减也是不一样的。所以,一些频率分量在传输过程中是减少的,收到的信号会失真。到达接收端的频率范围定义了绝对带宽(Absolute Bandwidth)。有兴趣的读者可以在Stallings(2000)文献中找到有关时间和频率领域概念的更多细节。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




