逻辑代数是研究逻辑关系的一门科学,是分析和设计数字电路的数学工具。它是由数学家乔治·布尔(George Boole)创立的,通常又称为布尔代数。逻辑代数表示的不是数量间的关系,而是逻辑关系。逻辑代数中自变量和函数的两种可能状态分别用符号“1”和“0”表示,因而又称为双值代数。逻辑代数中的“0”和“1”不代表数量的大小,而代表两种对立的状态。如“接通”与“断开”,“高电位”和“低电位”等。
1.逻辑运算的基本定律、常用公式与顺序规则
(1)基本定律
1)常量与常量的关系:
0·0=0 (7-10) 1+1=1 (7-11)
0·1=0 (7-12) 1+0=1 (7-13)
1·1=1 (7-14) 0+0=0 (7-15)

2)常量与变量的关系:
A·1=A (7-18) A+0=A (7-19)
A·0=0 (7-20) A+1=1 (7-21)

3)与普通代数相似的定律:
交换律 A·B=B·A (7-24)
A+B=B+A (7-25)
结合律 (AB)C=A(BC) (7-26)
(A+B)+C=A+(B+C) (7-27)
分配律 A(B+C)=AB+AC (7-28)
A+BC=(A+B)(A+C) (7-29)
4)逻辑代数的特殊定律:
同一律 A·A=A (7-30)
A+A=A (7-31)
摩根定律 

还原律 
(2)常用公式
公式A
证明 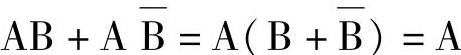
可见,若两个乘积项中分别包含了B、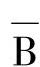 ,而其他因子都相同时,则可利用公式A将这两项合并成一项,并消去变量B。
,而其他因子都相同时,则可利用公式A将这两项合并成一项,并消去变量B。
公式B A+AB=A (7-36)
证明 A+AB=A(1+B)=A
公式B说明,在一个与或表达式中,如果一个乘积项是另外一个乘积项的因子,另外一个乘积项则是多余的。
公式C
证明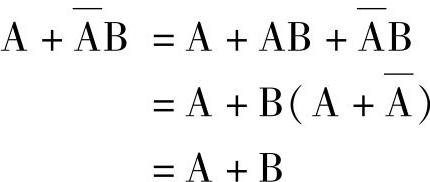
公式C说明在一个与或表达式中,如果一个与项的非是另一个与项的因子,则这个因子是多余的。
公式D
证明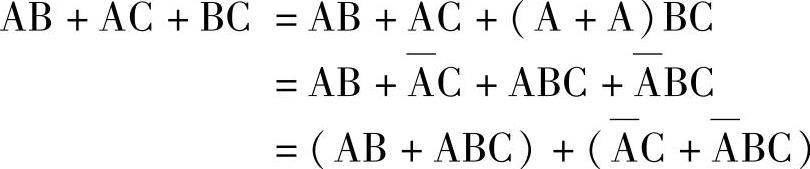
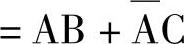
推论 
证明 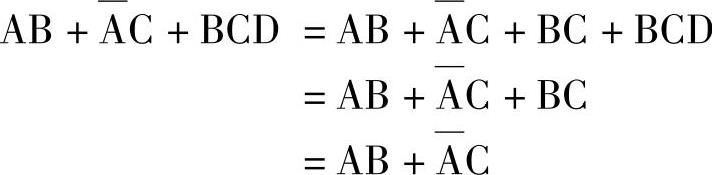
式(7-38)和式(7-39)说明在一个“与或”表达式中,如果两“与”项中,一项包含了某个原变量A,另一项包含它的反变量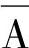 ,而这两项的其余因子都是第三个“与”项的因子,则第三项是多余的,该项称为冗余项。公式D称为冗余定理。
,而这两项的其余因子都是第三个“与”项的因子,则第三项是多余的,该项称为冗余项。公式D称为冗余定理。
(3)基本规则
1)代入规则:将公式中的变量以一个函数代之,公式仍成立。例如: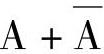
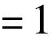 以B+C代替A仍成立,则
以B+C代替A仍成立,则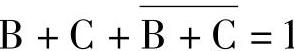 。
。
2)对偶规则:将逻辑公式中的“·”变“+”、“+”变“·”、“0”变“1”、“1”变“0”,则得到原式的对偶式仍成立。例如: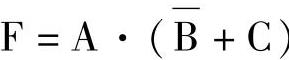 ,则F的对偶式
,则F的对偶式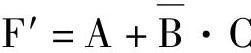 。
。
如果两个逻辑式相等,则它们的对偶式也一定相等。例如: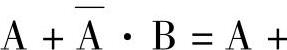
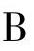 成立,那么它的对偶式A·(A+B)=A·B也成立。值得注意的是在变换中函数的运算顺序不能改变。
成立,那么它的对偶式A·(A+B)=A·B也成立。值得注意的是在变换中函数的运算顺序不能改变。
3)反演规则:将函数F中的“·”变“+”,“+”变“·”,“0”变“1”,“1”变“0”,原变量变成反变量,反变量变成原变量,则得到原函数的反函数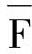 。同样应注意函数的运算顺序不能改变。例如:
。同样应注意函数的运算顺序不能改变。例如: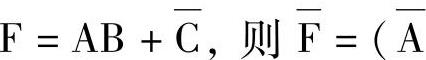
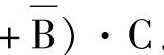 ,而不能写成
,而不能写成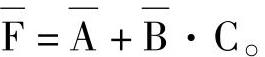
(4)顺序规则 和一般代数一样,逻辑代数也按一定的先后顺序进行运算。首先进行括号内的一级运算,按先小括号、再中括号、后大括号的顺序,然后再进行括号外一级的运算。在同级运算中要先“与”后“或”。
例如: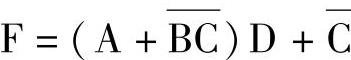 ,应先进行括号内
,应先进行括号内 的运算,本级内先进行
的运算,本级内先进行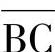 ,得出结果后再和A或,后进行括号外级运算,即将括号内的运算结果先和D与,再和
,得出结果后再和A或,后进行括号外级运算,即将括号内的运算结果先和D与,再和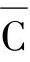 或。运算顺序亦是电路的实现顺序。
或。运算顺序亦是电路的实现顺序。
2.逻辑函数的基本概念、表示形式与转换
(1)基本概念 仅有两种取值的变量(即二值量)称为逻辑变量。这两种值可以用逻辑0和逻辑1表示。如果输入逻辑变量A、B、C……的取值确定之后,输出逻辑变量Z的值也被唯一地确定了,那么我们就称Z是A、B、C……的逻辑函数,并写成
Z=f(A、B、C……)
逻辑函数是把事件结果视为因变量(函数)用F或Z表示,把影响事件的诸多因素视为自变量,用A、B、C等表示,按相应的因果关系组成函数式子。
(2)表示形式
逻辑函数常用的表示方法有真值表、表达式、逻辑图、卡诺图和时序图(又称为波形图)五种形式。因为都表示同一函数,所以可以互相转换。
1)真值表:描述逻辑函数各个变量取值组合和函数值对应关系的表格叫做真值表。每一个输入变量为“0”、“1”两种取值,几个输入变量有2n个不同的取值组合。如果将输入变量的全部取值组合和相应的输出函数值一一列举出来,即可得到真值表。
例如:列写供3人(A、B、C)投票用的投票机的真值表,当二人或二人以上同意时,决议通过,用灯亮F表示。首先列出实际问题的功能表,经赋值后取得真值表,见表7-11。
表7-11 由功能表求真值表
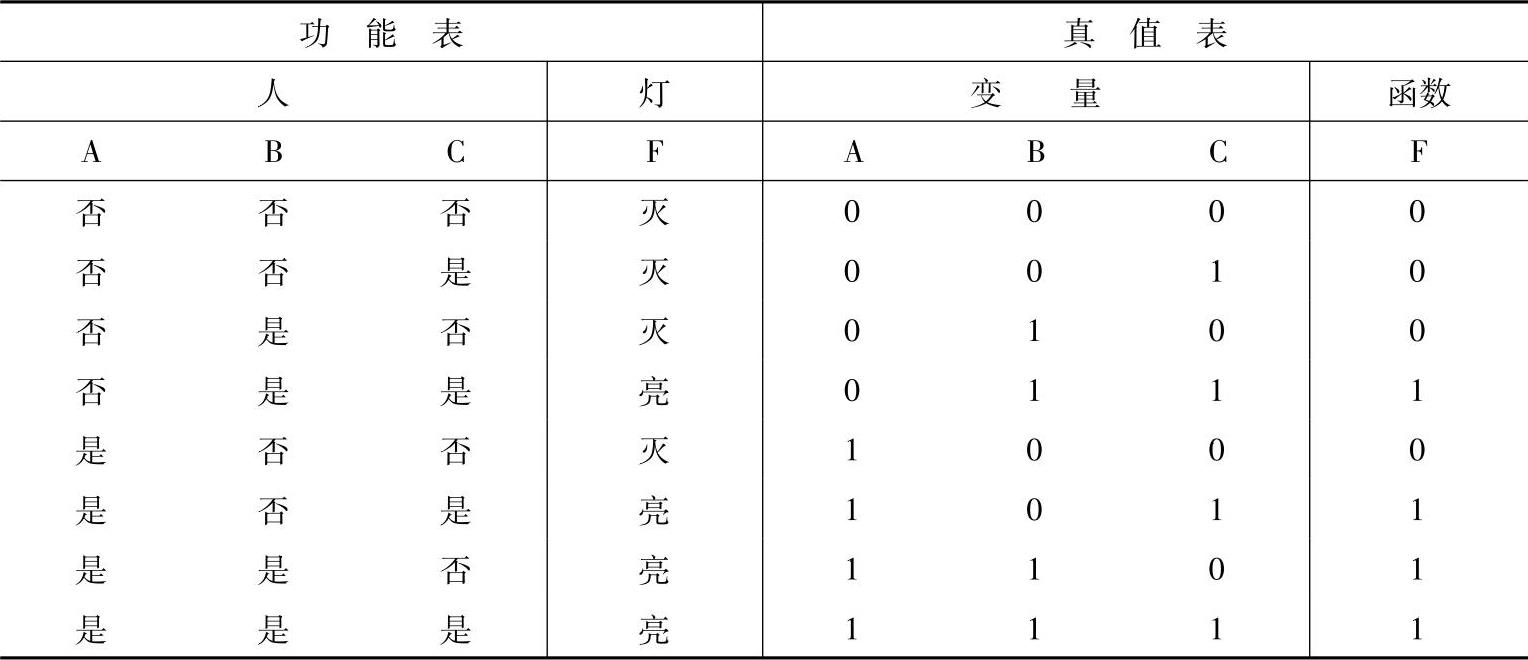
注:同意时用“是”表示,并赋值1,不同意用“否”表示,赋值0。
2)表达式:用与、或、非运算符号并按运算顺序规则联接的各变量之间的关系式称为逻辑表达式,简称表达式。
例如Z=(A+B)C+D。它的特点是书写方便,形成简洁,便于进行运算和化简,与逻辑图的关系较密切。
3)逻辑图:用逻辑符号表示各变量之间的关系的图称为逻辑电路图,简称逻辑图。它的特点是接近于工程实际,不同的逻辑符号有相应的器件对应,以便制作实际的数字电路。
4)时序图:表示各变量和函数在时间上的对应配合关系的波形图称为时序图。只有正确地绘制出时序图,才能全面深刻地理解各变量和函数的配合关系。
(3)转换方法
1)真值表转换为表达式。在真值表中,挑选出那些使函数值为1的变量取值组合,变量值为1的写成原变量,为0的写成反变量,这样对应于使函数值为1的每一个组合都可以写出一个乘积项,只要将这些乘积项加起来,就可以得到函数的标准“与或”式。
例7-15 由表7-12所示的真值表,试写出其函数表达式。
表7-12 例7-15真值表
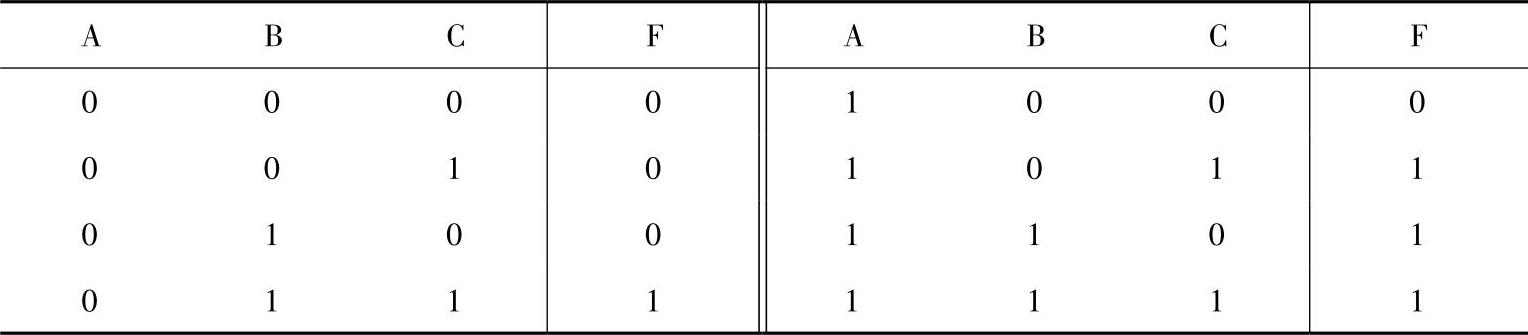
解 A、B、C有四组取值使F为1,它们分别是011、101、110、111。按照变量值为1的写成原变量,为0的写成反变量的求乘积项的原则,可得四个乘积项——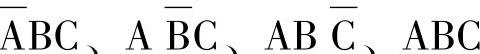 。将四个乘积项加起来所得的就是函数F的表达式,即
。将四个乘积项加起来所得的就是函数F的表达式,即
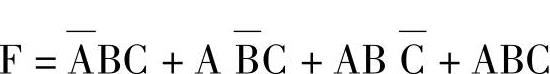
2)表达式转换成真值表。一个与或表达式可以转换成一张真值表。式中的一项(原变量读1,反变量读0)为表中F=1的一行或几行,式中未出现的变量组合,其F=0。在由表达式换成真值表时,要先将表达式化成与或形式,因为真值表仅仅和与或式有直接对应关系。
例7-16 列出函数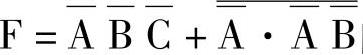 的真值表。
的真值表。
解 首先将函数化简成与或式 。由于函数中出现A、B、C,故为三变量函数,可列其真值表框架,见表7-13。
。由于函数中出现A、B、C,故为三变量函数,可列其真值表框架,见表7-13。
表7-13 例7-16真值表框架
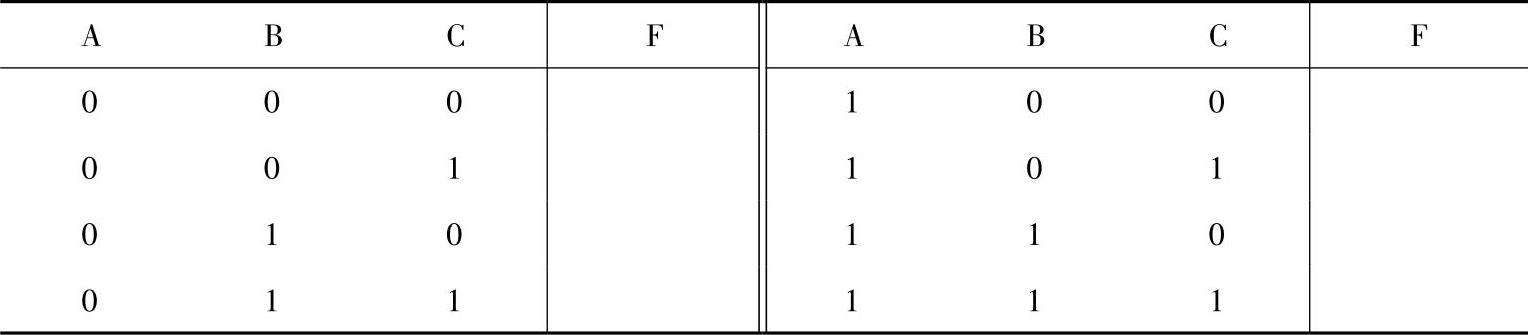
F值取决于与或式各项。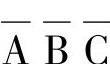 是最小项,对应取值000,则在表中变量取值000的对应F处填1;
是最小项,对应取值000,则在表中变量取值000的对应F处填1;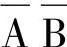 是非最小项,变量C没出现,所以C取任意值,则在表中对应A、B取值为0,0的所有行F处填1(已为1者不再填);项A亦是非最小项,故在A取1,对应表中后四行F值填1,式中各项已填完,余下的F值填0,其真值表见表7-14。
是非最小项,变量C没出现,所以C取任意值,则在表中对应A、B取值为0,0的所有行F处填1(已为1者不再填);项A亦是非最小项,故在A取1,对应表中后四行F值填1,式中各项已填完,余下的F值填0,其真值表见表7-14。
表7-14 例7-16真值表

3)真值表和卡诺图间的转换。真值表和卡诺图是一一对应关系,真值表中变量的一种取值组合,对应卡诺图中同编号的一块,表中此取值组合的函数值对应了图中该块内填写的值。反之亦然。
4)表达式和卡诺图间的转换。由于真值表和卡诺图的一一对应关系,故仅需将表达式化成与或式,根据与或式和真值表转换关系及真值表和卡诺图的转换关系,可跳过真值表直接得到卡诺图。
5)表达式转换成逻辑图。将表达式按运算的顺序以相应的逻辑符号代替运算符号,即可得到函数的逻辑图。表达式应是最简式,以便用最少的数字器件可靠地实现逻辑关系。由于同一函数关系可以有不同的表达式,因此函数的逻辑图不是唯一的。
6)逻辑图转换成表达式。由于一个逻辑符号对应一种逻辑运算,所以按信号流程可逐级写出表达式,直至输出,即可得到函数的表达式。要注意写信号流程时应加上必要的括号,以免出现错误。
7)表达式转换成时序图。其画法是将已知变量的变化波形图分成若干区段,使每一区段中各变量均为常数,并代入函数表达式计算,如果值为1,则在函数的相应区段内画成高电平,如果值为0,则画成低电平。当表达式关系较简单时,可根据逻辑关系直接画出时序图。
3.逻辑表达式的化简
(1)逻辑函数的五种表达式 同一逻辑函数,可以有五种不同形式的逻辑表达形式,即与或表达式、或与表达式、与非-与非表达式、或非-或非表达式和与或非表达式,其中与或表达式是基本形式。
例如某一个逻辑函数的五种表达式如下:
1)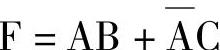 与或表达式。
与或表达式。
2)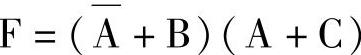 或与表达式。
或与表达式。
3)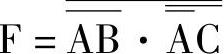 与非-与非表达式。
与非-与非表达式。
4)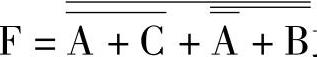 或非-或非表达式。(https://www.xing528.com)
或非-或非表达式。(https://www.xing528.com)
5)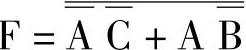 与或非表达式。
与或非表达式。
一般地,逻辑表达式越简单,相应的逻辑电路也越简单,所以对逻辑函数要通过化简求得“最简”的逻辑表达式。
所谓“最简”就是在不改变逻辑关系的情况下,首先乘积项的个数应该最少;其次在满足乘积项个数最少的条件下,要求每一个乘积项中变量的个数最少。逻辑表达式的化简主要有代数法和卡诺图法。
(2)代数法化简逻辑表达式
1)并项法:利用公式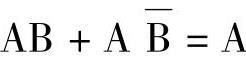 ,将两个乘积项合并成一项,并消去一个互反的变量。
,将两个乘积项合并成一项,并消去一个互反的变量。
例7-17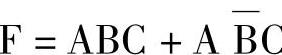
解
例7-18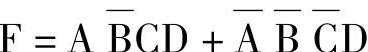
解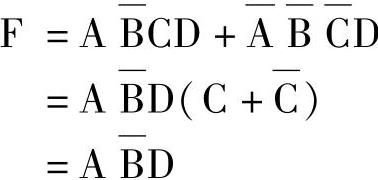
2)吸收法:利用公式A+AB=A吸收多余的乘积项。
例7-19 F=AB+ABCD
解 F=AB+ABCD=AB
例7-20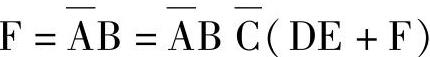
解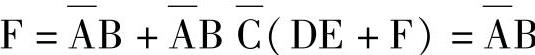
3)消去法:利用公式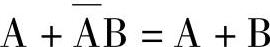 消去多余因子。
消去多余因子。
例7-21
解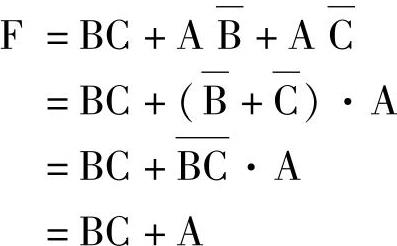
4)配项法:当表达式不能直接用上述公式化简时,有时可利用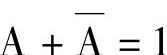 ,去乘某个缺少一个或几个变量的乘积项,然后将其拆成两项,再与其他项合并化简。
,去乘某个缺少一个或几个变量的乘积项,然后将其拆成两项,再与其他项合并化简。
例7-22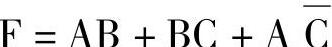
解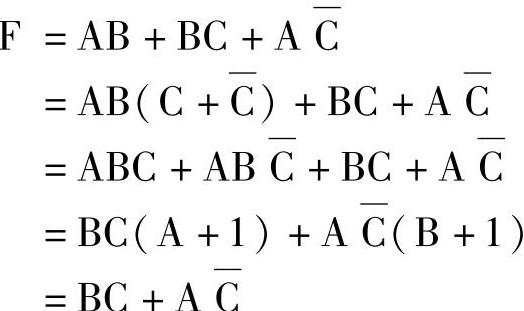
例7-23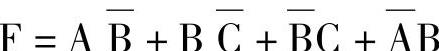
解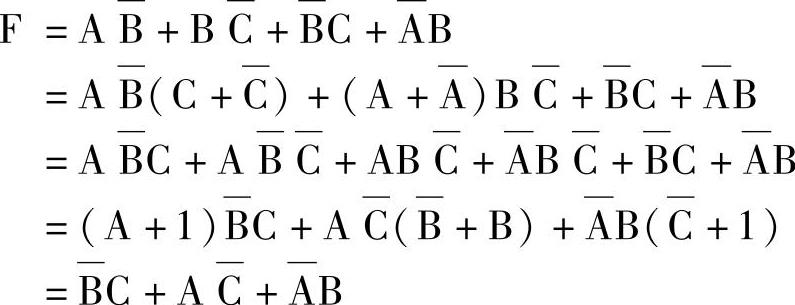
假如采用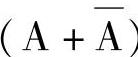 去乘
去乘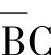 ,用
,用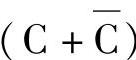 去乘
去乘 ,然后用代数法化简,则可得
,然后用代数法化简,则可得
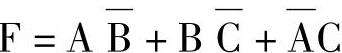
由此可知,经代数法化简得到的最简与或表达式,有时不是唯一的。
(3)卡诺图法化简逻辑表达式
1)卡诺图的概念:就是将逻辑函数表达式中各最小项按相邻原则相应地填入一个特定的方格图内,此方格图就称为卡诺图。
①关于最小项:
a.最小项的基本概念:如果每个变量或以原变量或以反变量的形式在项中出现且仅出现一次,则此与项即称为这几个变量的一个最小项。
对于n个变量的逻辑函数,其全部最小项数目为2n个。任何一个逻辑函数都可以表示成若干个最小项之和,通常称为最小项表达式。
b.最小项的性质:
●对于任意一个最小项,只有一组变量的取值使它的值为1,而在其他组取值时,它的值都是0。并且最小项不同,使它的值为1的那一组变量取值也不同。
●任意两个最小项的乘积为0。
●变量在任意取值条件下,全部最小项之和总是为1。
c.最小项编号:二变量逻辑函数的取值组合共有四种情况。若将取值为0的变量用反变量表示,取值为1的变量用原变量来表示,如AB,取值为00时写为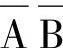 ,依此类推,可形成表7-15中的全部最小项,将其编号,方法如下:最小项
,依此类推,可形成表7-15中的全部最小项,将其编号,方法如下:最小项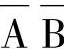 ,因为它的取值为00,相当于十进制中的0,用符号m0表示,其偏号为0。其余类推。
,因为它的取值为00,相当于十进制中的0,用符号m0表示,其偏号为0。其余类推。
表7-15 二变量最小项编号
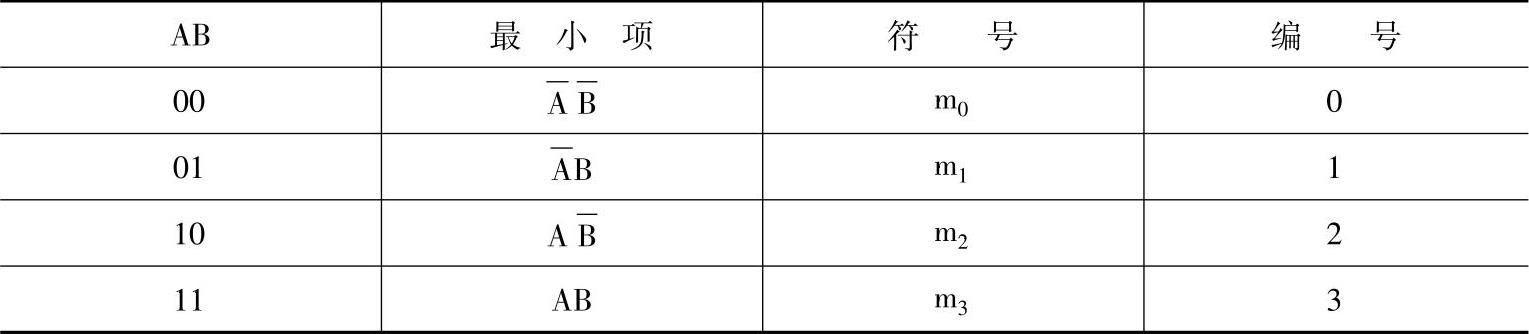
同理,三变量、四变量最小项编号见表7-16、表7-17。
表7-16 三变量最小项编号
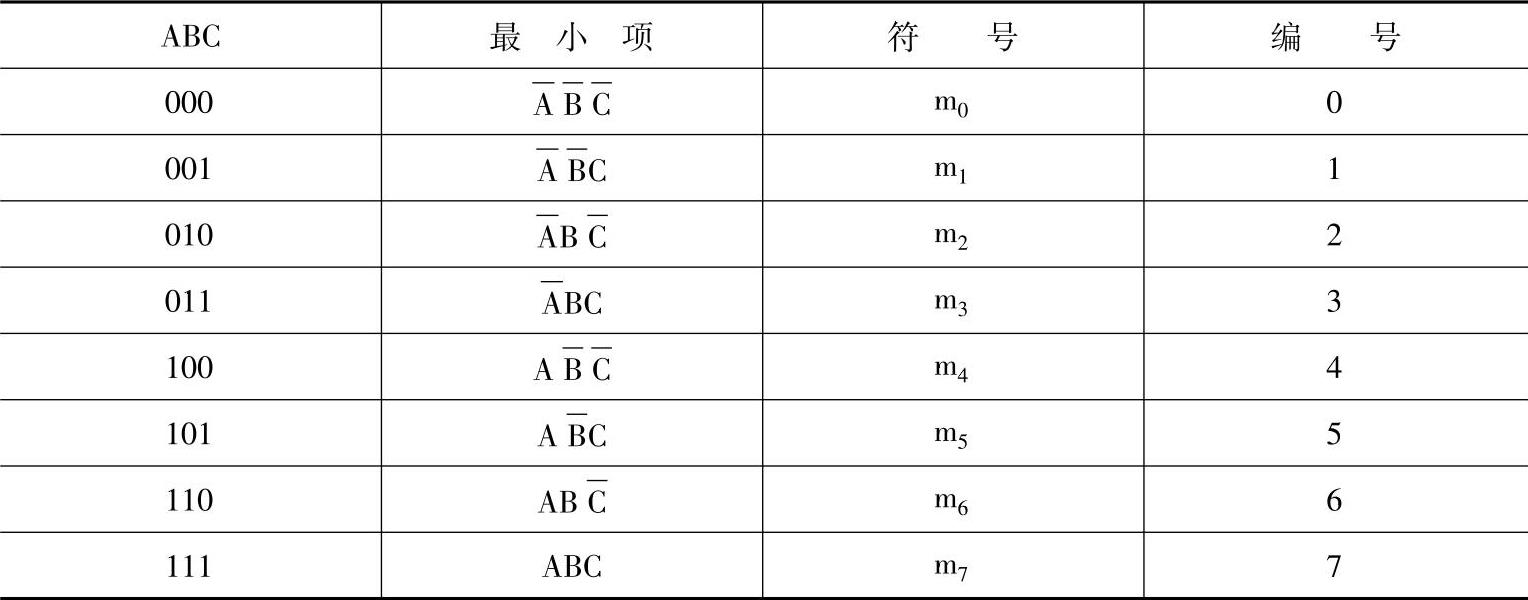
表7-17 四变量最小项编号
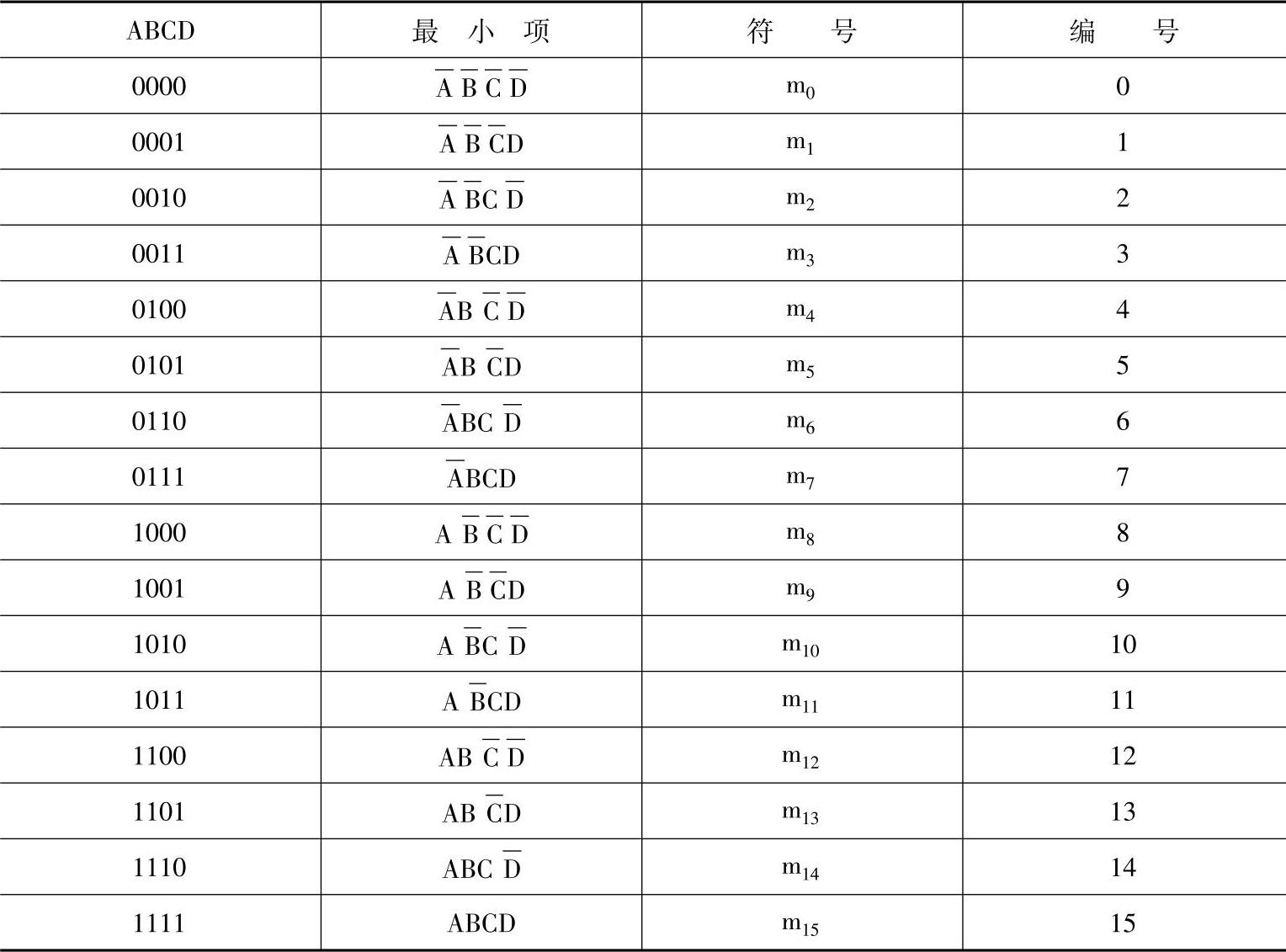
②关于卡诺图:根据变量的数目n,卡诺图中小方格的数目应为2n个,每个小方格对应一个最小项,卡诺图行、列坐标变量的取值是按相邻性原则组成的。“相邻性”即相邻两个小方格所表示的两个最小项,只有一个变量互反,其余变量都相同。
a.二变量卡诺图。二变量最小项数为2n=4,需要用四个小方格按相邻性原则排列起来。如图7-26a所示,把变量A、B分别标注在方格图的左上角斜线两边。若把原变量作为1,反变量作为0,则方格中各变量组合可视为二进制数,如图7-26所示。
b.三变量卡诺图。三变量有23=8个最小项,把三变量A、B、C分为A和BC各一组,分别标注在方格图左上角斜线两边,方阵的行坐标变量为A,
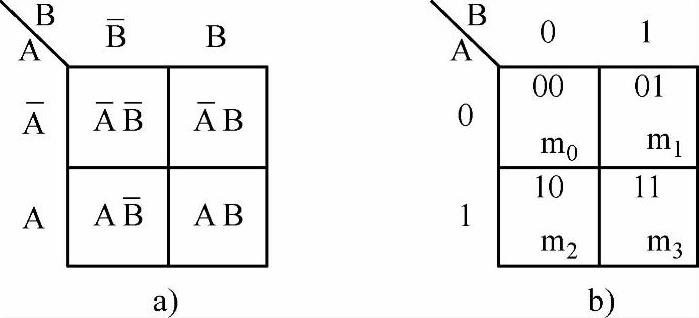
图7-26 二变量卡诺图
第一行排 ,用“0”表示,第二行排A,用“1”表示。方阵的列坐标排变量BC,四列由左至右的顺序是:
,用“0”表示,第二行排A,用“1”表示。方阵的列坐标排变量BC,四列由左至右的顺序是: 、
、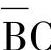 、BC、
、BC、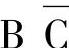 ,分别用00、01、11、10表示。三变量卡诺图如图7-27所示。
,分别用00、01、11、10表示。三变量卡诺图如图7-27所示。
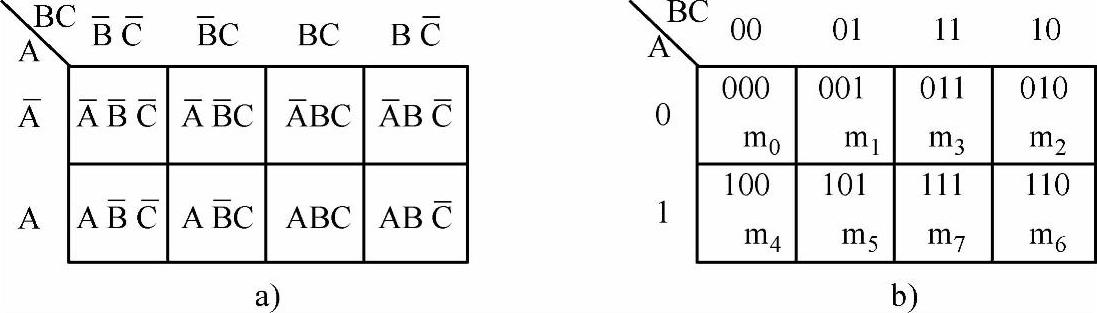
图7-27 三变量卡诺图
c.四变量卡诺图。四变量有24=16个最小项。把四变量分成AB和CD两组,每组变量都是两变量,它们的取值顺序均为00、01、11、10以保证最小项的相邻性。注意方格图最上与最下、最左与最右对应的小方格也是逻辑相邻的。实际上凡与中心轴对称的最小项均为逻辑相邻项。四变量卡诺图如图7-28所示。
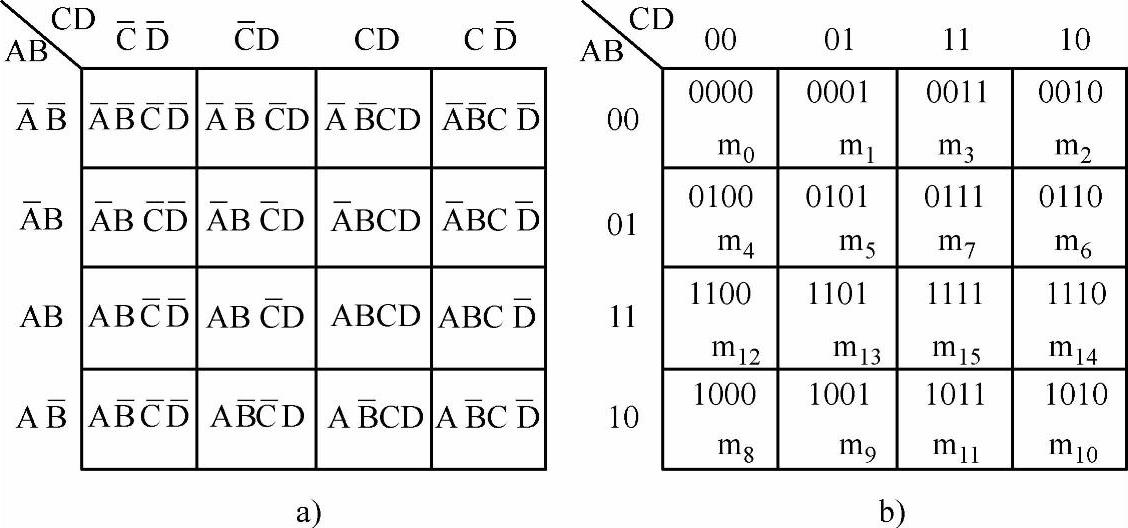
图7-28 四变量卡诺图
2)卡诺图表示法:将函数之值填入变量卡诺图即得到函数的卡诺图。其步骤如下。
第一步:由逻辑表达式所包含的变量数(n个不同的字母),确定画出n变量空白卡诺图。
第二步:逻辑函数表达式一定是与或式,如果原来表达式不是与或式,要用公式变换成与或式。
第三步:在卡诺图中,把表达式中各乘积项所包含的最小项都填上1,其余的填0或不填,就可以得到逻辑表达式的卡诺图。
例7-24 画出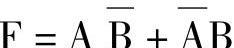 的卡诺图。
的卡诺图。
解 因表达式包含两个变量A、B,所以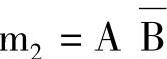 和
和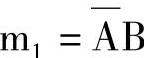 就是两个最小项。把这些最小项在空白卡诺科的对应格中填1,其余格不填,可得如图7-29所示的卡诺图。
就是两个最小项。把这些最小项在空白卡诺科的对应格中填1,其余格不填,可得如图7-29所示的卡诺图。
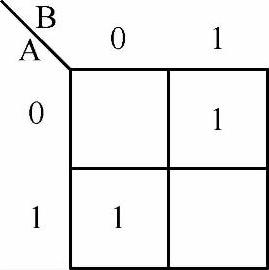
图7-29 例7-24卡诺图
例7-25 用卡诺图表示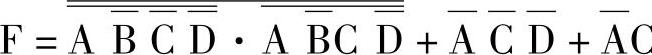 。
。
解 将原表达式用公式化成与或式。
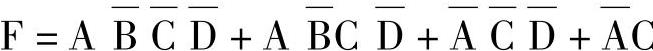
画出四变量卡诺图。当A、B、C、D取值为1000时,满足与项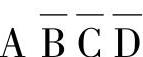 ,故其值为1,函数值F=1,则在变量卡诺图1000对应的小方格内填1;同理,对于与项
,故其值为1,函数值F=1,则在变量卡诺图1000对应的小方格内填1;同理,对于与项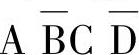 满足它的取值的A、B、C、D应为1010,所以在其对应的小方格内填1。与项
满足它的取值的A、B、C、D应为1010,所以在其对应的小方格内填1。与项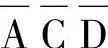 是非最小项,其中变量B没出现,所以和B无关。只要A、C、D取值000,则有函数值F=1,可在对应的0000和0100两小方格中填1;同时
是非最小项,其中变量B没出现,所以和B无关。只要A、C、D取值000,则有函数值F=1,可在对应的0000和0100两小方格中填1;同时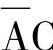 项,只要A、C取值为01,则F=1,其对应的四块小方格0010、0011、0110、0111中都填1(如果重复时只填一个1也可以),填完了所有的与项,剩下的空格其函数值为0,可以不填,得到函数卡诺图如图7-30所示。
项,只要A、C取值为01,则F=1,其对应的四块小方格0010、0011、0110、0111中都填1(如果重复时只填一个1也可以),填完了所有的与项,剩下的空格其函数值为0,可以不填,得到函数卡诺图如图7-30所示。
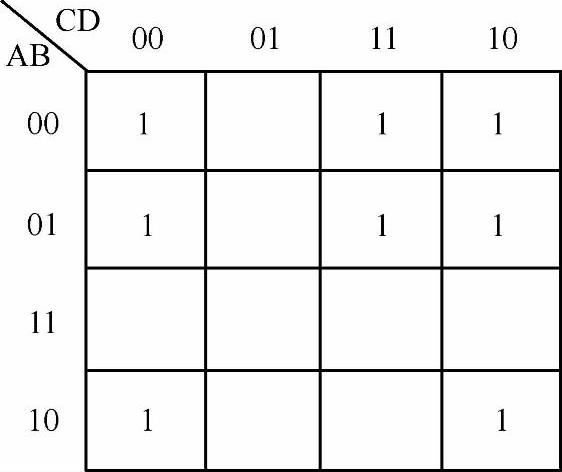
图7-30 例7-25卡诺图
3)用卡诺图化简逻辑表达式:在卡诺图中相邻小方格所对应的最小项具有相邻性,即在两个相邻的小方格中除仅有一个变量“互反”外,其他变量都相同。因此在卡诺图化简逻辑函数中,利用
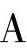 的公式消去互反变量,保留相同变量,使函数得到化简。
的公式消去互反变量,保留相同变量,使函数得到化简。
①化简步骤:先画出逻辑函数的卡诺图,再合并最小项。
②合并最小项的规律:
a.相邻两个最小项,可消去一个互反的变量,复合为一个乘积项,此乘积项由两个最小项中公有的变量组成。注意由两端组成的两个相邻小方格不能画成封闭的包围圈,因为每一个包围圈表示一个乘积项。
b.相邻四个最小项,可消去两个互反的变量,复合为一个乘积项,此乘积项由四个最小项中公有的变量组成。
c.相邻八个最小项,可消去三个互反的变量,复合为一个乘积项,此乘积项由八个最小项的公有变量组成。
③用卡诺图化简逻辑函数的原则:
a.圈的个数尽量少。圈越少,乘积项越少,所用与门也越少。
b.圈尽量大。圈越大,消去的变量越多,所用与门输入端越少。
c.有些方格可以多次被包围,但每个包围圈至少要包含一个新项(即未被其他圈圈过的),否则它是多余的。
d.必须把全部的“1”圈完,不能漏掉某一项“1”。无相邻关系的方格,单独画成一个包围圈。
e.在对“1”圈卡诺图时,圈内不能有含“0”的项。
f.将各包围圈所得到的乘积项进行逻辑加,便可得到最简与或表达式。
例7-26 用卡诺图化简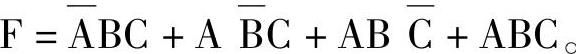
解 (1)画出函数F的卡诺图。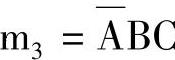 ,
,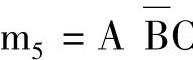 ,
,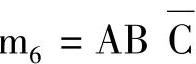 ,m7=ABC是四个最小项,其卡诺图如图7-31所示。
,m7=ABC是四个最小项,其卡诺图如图7-31所示。
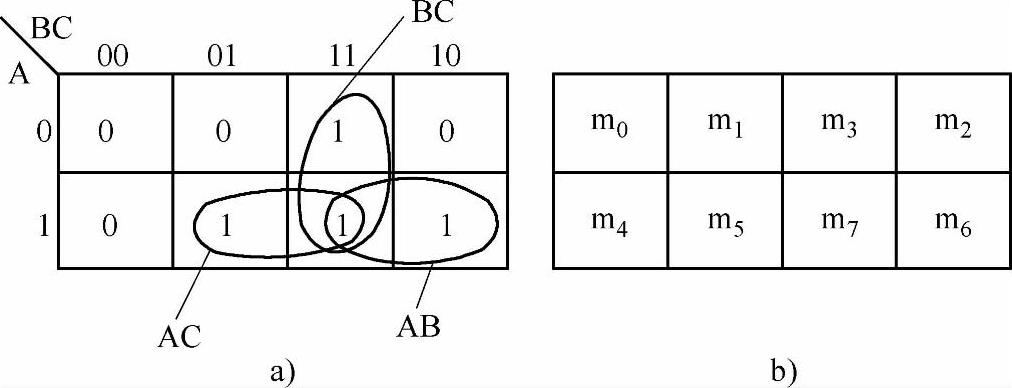
图7-31 例7-26卡诺图
(2)合并最小项。用环把可合并的最小项圈起来,如图7-31a所示。
(3)根据圈定的各个环,可写出最简与或表达式为
F=AB+BC+AC
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




