探秘武器系统的控制原理

1.火控问题的描述

1）瞄准矢量

瞄准线是指以观测器材回转中心为始点，通过目标中心线的射线。以观测器材回转中心为始点、目标中心为终点的矢量称为瞄准矢量。瞄准矢量常用球坐标（D，β，ε）表示，其中D、β、ε分别表示目标现在点的斜距离、方位角、炮目高低角。跟踪线是指目标自动跟踪器的基准点与目标探测位置的连线。在目标跟踪过程中，随时探测出目标在空间的有关位置，并由此控制瞄准线，以实现对目标的自动跟踪。武器线是指以武器身管或发射架回转中心为始点，沿膛内或发射架上弹头运动方向所构成的射线。在搜索和跟踪时，瞄准线与武器线处于同轴控制的状态。而当系统射击时，两者之间在高低和方向上均有一个按射击诸元装定的角度差。射击线是指为保证弹头命中目标，在武器发射瞬间，武器线所必需的指向。现在点是指将目标视为一个点，在弹头每次发射瞬间，目标所处的空间点。未来点又称命中点，是指目标与弹头（视为一点）相碰撞的空间点。射击诸元主要指射击线在大地坐标系中的方位角βg和射角φg。弹道的弯曲、气象条件影响、目标的运动、武器载体的运动都会导致瞄准矢量与射击线不一致，射击线相对瞄准矢量的夹角定义为空间提前角。空间提前角一般分解为方位提前角和高低提前角。空间提前角取决于弹头的外弹道特性与目标和武器载体的运动状态。瞄准矢量、射击线与空间提前角的相互关系如图10.2所示。未来点是相对现在点而言的，在火控问题有解范围内，二者一一对应。武器线与射击线一般是不重合的，存在偏差，称为射击诸元误差。只有当射击诸元误差小于希望值时，才允许射击。

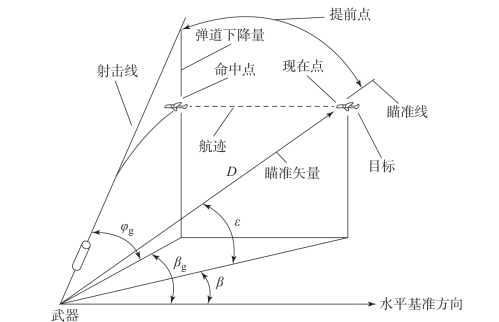
图10.2　瞄准矢量、射击线与空间提前角的相互关系

2）武器射击控制过程

实际火控系统的原理各不相同，但对武器射击控制的过程却大致相同。图10.3所示为车载武器射击控制的一般过程，图中各方块是与系统有关的功能块。

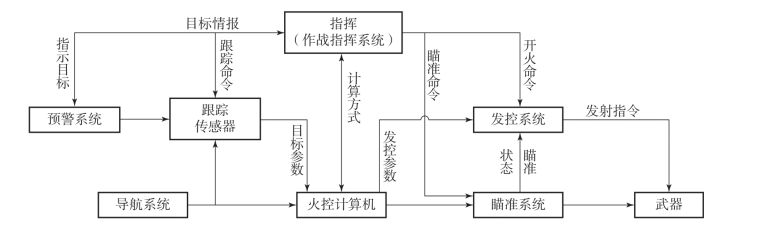
图10.3　车载武器射击控制的一般过程

预警系统主要负责对指定地域、空域进行搜索发现目标，经作战指挥系统以目标指示命令形式传送到观测跟踪传感器和火控计算机。跟踪传感器立即对指定的目标进行捕捉、跟踪，不断精确地测量目标坐标，并自动向火控计算机提供目标信息。火控计算机接收跟踪信息的同时，还接收导航系统的武器运动和姿态信息、接收弹道气象参数等，准确计算出命中目标所需的射击（导引）诸元，以及辅助作战的战术数据。在向操作手和指挥员显示有关数据的同时，还连续地向武器瞄准系统发送射击（导引）诸元。武器瞄准系统在接收到火控计算机输出的射击（导引）诸元后，以自动或半自动方式控制武器完成实时跟踪瞄准，或向武器制导部件装定预定控制参数，保证武器发射后战斗部能准确地到达命中目标区域。武器发射控制系统直接由射击指挥员的命令控制，按指定的射击方式适时控制武器开火射击，但武器能否开火还受到武器瞄准系统的瞄准状态、火控计算机计算的发控参数、武器的射击范围等因素的限制和约束，以确保安全、可靠地实施发射。

2.火控命中问题及其解算

1）火控命中问题

火控系统的主要作用是自动或半自动地解决在实际条件下火炮射击命中目标问题。命中是指发射的弹丸准确地与目标相碰撞。对于静止目标，命中就意味着发射的弹丸准确地达到目标所处的空间位置。对于运动目标，命中就意味着发射的弹丸与目标同时达到空间未来的同一位置。

火炮发射弹丸总是希望命中目标，因此必须准确知道目标当前的位置及其运动状态（运动速度和加速度及其运动方向等）、当前武器相对目标的位置及其运动状态（运动速度和加速度及其运动方向等）、弹丸的飞行规律，以及各种因素影响规律。也就是说，为解决射击命中问题，需要研究火炮和目标的运动规律以及弹丸在大气空间的运动特性。

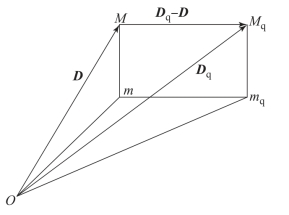
图10.4　火控命中问题

火控命中问题就是如何利用火控系统的获取信息能力、处理信息能力和操控能力保证弹丸准确地命中目标，就是以火炮发射时刻目标所在位置（即现在点M的位置）为初值，求取弹丸飞行时间tf后与目标相遇的提前点Mq的位置，如图10.4所示。图中，D为当前目标距离矢量；Dq为提前点距离矢量；Dq-D为距离差矢量；m为目标当前点在水平面上的投影；mq是提前点在水平面上的投影。

在火控系统数学模型中，主要解决两方面问题：一方面是目标的运动规律；另一方面是弹丸的运动规律。

（1）目标状态估计。

目标状态估计，首先是测量当前目标坐标，包括测定目标相对火炮的角度（称为测角，又分为高低角和方位角测定）和测定目标相对火炮的距离（称为测距）。

对于运动目标，尽管可以测量到火炮发射时刻目标所在的位置（即现在点M的位置），但是弹丸在飞行时间tf后与目标相遇的提前点Mq的位置并不知道。因此，需要由目标在当前M的状态估计经过弹丸飞行时间tf后的未来点Mq的位置。尽管战场上的情况会千变万化，在有限的系统反应时间及弹丸飞行时间内，目标的任意机动受到地形和动力的限制。所以在许多火控系统中，为了简化目标运动状态的求解，在一定条件下均按“匀速直线运动”对目标的运动规律进行假定或估计。在火控系统中，实际上是以某个采样周期，测量出目标的序列运动参数，以此建立反映目标运动规律的状态方程，再以现在点M处的目标状态为初值，求取弹丸在飞行tf时间后目标到达Mq时的状态（位置）。由于在这一动态过程的各个环节上必然存在随机噪声，因此对机动目标的解命中问题就成为目标在提前点的位置或状态的最佳预测估计问题，这也是典型的跟踪滤波问题。

（2）火控外弹道模型。

弹丸的运动规律是通过外弹道模型来估计的，并把计算结果转换为火炮的射击诸元，根据射击条件偏差量来计算射击诸元修正量。根据不同的条件，火控外弹道模型应是多种多样的，目前火控系统使用的火控外弹道模型有5种类型：外弹道微分方程组、弹道诸元的解析表达式、射表、射表诸元的逼近表达式、射表与弹道微分方程组联合使用。

在外弹道微分方程组中，包含许多变量与参数，这些变量与参数涉及气象诸元、空气动力系数、弹丸的几何与质量分布参数、弹丸质心的运动参数及绕质心的角运动参数、地球与地形有关参数等。弹道微分方程组又分为质点外弹道微分方程组、修正质点外弹道方程和刚体外弹道方程等。在工程应用中，考虑计算精度与计算速度的要求，提出了修正质点外弹道模型。外弹道微分方程组作为火控外弹道模型，可以考虑多种因素，可以提高计算精度。但是弹道微分方程组比较复杂，对多种参数和初始条件有很大的依赖性，参数的精度将直接影响计算结果的精度。

将弹道诸元的解析表达式作为火控外弹道模型是最理想的，因为它的函数关系表达明确、计算精度高、计算速度快。问题的关键是弹道微分方程组积分成简洁的解析表达式并不是一件容易的事情，只有在一些特殊条件下，利用弹道参数变化的某些特殊性，才能消除弹道方程组联解性，分离变量，使微分方程能单独积分，得到解析表达式。可见，解析表达式作为火控外弹道模型，在使用上有较大的局限性。

火控计算机的一项首要计算任务是在已知目标距离D后，根据外弹道微分方程组解算出火炮的射角φ和弹丸飞行时间tf。火控系统中的外弹道解算任务是外弹道微分方程典型的初值问题的逆问题，即原初始条件中的重要参数射角φ成了求解对象，这给外弹道问题的求解增加了困难。在当前的火控系统工程实践中，采用火炮射表逼近的方法来进行外弹道问题的近似解算。

射表是针对特定的弹、炮、药，在实际条件下使用的，含有所需射击诸元的数字表或图表。射表给出了在标准条件下射击诸元、弹道诸元、修正诸元、散布诸元、辅助诸元之间关系。射表编制一般采用理论计算与射击试验相结合的办法。火控计算机在有了距离D以后，所求解的是射击诸元和弹丸飞行时间。利用射表，采用插值法，就可以计算出射击诸元和弹丸飞行时间。

2）火控命中问题的解算

（1）给定距离射击诸元求解。

这是在火控系统射击诸元求解过程中的弹道问题，却不具备方程组所需的初始条件，已知的只是弹道起点和预期目标点的部分参数，这是典型的两点边值问题。如何从边值条件式出发，求解出火炮射击时所需的射击诸元和弹丸飞行时间，正是火控系统中数值求解外弹道问题的内容。

通常，以弹道轨迹的某些物理特性为依据，采用步长自动选择算法的迭代-修正法，可将边值问题化为初值问题迭代求解：

①预先估计瞄准角。

②按初值问题求解外弹道微分方程组。

③根据第j步落点诸元进行瞄准角修正。

④步长h的自动选择。

⑤判断迭代完成的条件。

（2）目标匀速直线运动条件下的命中问题求解。

已知目标现在位置的坐标为（D，β=0，ε），目标当前运动速度为v。在采用“匀速直线运动”基本假定的前提下解命中问题，空间矢量如图10.5所示。可以建立包含3个方程的空间几何方程组，其中包含4个未知量（Dq、εq、βq和tf），由于未知量多于方程数，因此还需寻找新的关系式。由射表可知，弹丸的飞行时间tf可看作提前点坐标Dq的函数，即得补充方程：tf=f（Dq）。如果将补充方程代入基本方程组，就可以解出命中问题。结合外弹道求解，即可求解出火炮射击时所需的射击诸元。

（3）行进间射击活动目标时的命中问题求解。

已知目标现在位置点为m，载体速度矢量为vT，目标相对载体速度为vR。在采用“匀速直线运动”基本假定的前提下，引入相对运动，解命中问题如图10.6所示。图中的mq1点为一个虚拟提前点（或称相对提前点）。当载体不动时，以这一点为提前点，是完全可以实现弹丸与目标相遇的。当载体运动时，弹丸和目标在空间的实际相遇点并不是mq1点，而是提前点mq2点，因此，行进中的武器应向mq2点射击才能真正命中目标，即相对提前点mq1为所求点。同前，可以建立包含3个方程的空间几何方程组，其中包含4个未知量（Dq1、εq1、βq1和tf），未知量多于方程数，还需寻找新的关系式。由射表知，弹丸的飞行时间tf可看作提前点坐标Dq1的函数，即得补充方程：tf=f（Dq1）。如果将补充方程代入基本方程组，就可以解出命中问题。结合外弹道求解，可解出火炮射击时所需的射击诸元。实际上，这一差别主要来源于载体的速度矢量vT，考虑到v=vT+vR，不难求取实际提前点mq2。？(www.xing528.com)

图10.5　匀速直线运动解命中问题空间矢量

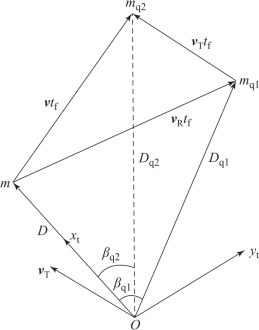
图10.6　载体行进间射击活动目标矢量

（4）解命中问题的数值计算方法。

解命中问题的数量方程组大都是三角函数的超越函数方程组，统称为非线性方程组，除了极个别情况下可解析求解外，通常要借助计算装置或数值计算方法进行求解。

在模拟式火控系统中，为了联合求解m个方程组成的方程组，通常由m个“解算分系统”构成，其中的每一个分系统，又皆由解算装置和伺服系统两部分组成。m个解算分系统协同工作，即可联立求解3个方程，得出提前点的m个待求量。设联立方程组的通式为fk（λi，xj）=0，i=1，2，…，n，j，k=1，2，…，m，其中λi为已知量（如现在点坐标、目标运动参数等），xj为待求量（即提前点坐标等）。

在现代的数字式火控系统中，可以采用数值计算的方法进行求解，这使整个解命中问题系统的面貌大为改观，这时既不需要专门的解算装置，也不需要附加伺服系统对稳定性起调节作用。同时，围绕模拟计算机解命中问题系统所展开的许多理论分析也自然失效，而需要以系统现在所选用的计算方法为背景，重新对系统的稳定性、动态特性等系统特性进行理论分析。可以认为，解命中问题的解算过程与理论分析方法的不同，构成了数字式火控系统在理论上区别于模拟式火控系统的重要方面。

为了便于数值求解的描述，将命中问题方程组改写为fk（xj）=0，j，k=1，2，…，m。对于此类非线性方程组，一般运用数值计算方法求解。常用的数值计算方法有两类：一类是求解由方程式组构造成的模函数极小值的方法；另一类属于线性化的方法。

3.火控系统修正

火炮实际的射击条件与标准条件经常不同。实际射击条件下的弹道诸元与标准条件的相应诸元之差称为修正量。射表是在标准条件下制成的，用射表求射击诸元时就应考虑修正。修正量计算是火控系统中又一个重要的计算任务。

从火炮射击的需要出发，在火控系统中所选择的修正诸元为瞄准角α、方向角β、射击距离D。修正量的计算公式是火控系统数学模型的一部分，而计算修正量的方法有求差法、微分法和以射表数据为依据的曲线拟合法。

以基本瞄准角α0为例。在基本问题中，它是阻力函数K、初速v0、射击距离D等参数的函数，即

α0=α0（K，v0，D，λ1，λ2，…）

假设实际射击条件下诸参数的增量为ΔK、Δv0、ΔD、…，则α0的修正量求差法计算式为

Δα0=α0（K+ΔK，v0+Δv0，D+ΔD，λ1+Δλ1，λ2+Δλ2，…）-α0（K，v0，D，λ1，λ2，…）

该式是直接按修正量的定义求出的，故是计算修正量最准确的算式。

实际上，上式中右端第一项很难求出，常常要借助微分法简化求解。当诸参数的增量不大时，将α0计算式在标准条件下按泰勒级数展开，略去高于增量一次项的部分后，即可得到α0修正量的微分法计算式：

由于微分法是泰勒展开式的简化计算式，未考虑各参数变化的相互影响，因此精度不是很高，但在很多情况下它是可行的方法，因而应用较多。

火炮射表中，包含大量修正量数据，这里所选择的修正诸元是距离D和方向角β。为利用这些数据进行修正量计算，可采用自动查表法和曲线拟合法，最常用的是曲线拟合法。然而，曲线拟合法在物理概念上不够直观，也不易分析各参数之间的影响。

1）气象条件及其修正

气象条件直接影响射弹弹道，气温与空气密度的改变影响弹道的阻力函数，横风影响弹道散布，纵风影响射弹射程。气象条件的选取将直接影响射弹的射击精度。

目前，我国炮兵使用的射表、弹道表及气象观测与计算所使用的仪器、图线等都是按标准气象条件制定的。武器的外弹道性能设计与比较、标准弹道的计算与数据处理也都以标准气象条件为准。

（1）地面标准值。我国炮兵标准气象条件：气温TON=288.9 K，气压pON=100 kPa，空气密度ρON=1.206 kg/m3，水蒸气分压aON=846.6 Pa，相对湿度f=50%。

（2）气温、气压、密度随高度的变化。

当弹道高y≤9 300 m时，气温T=TON-0.006 328y，气压p=pON（1-2.190 25×10-5y）5.4，空气密度ρ=ρON（p/pON）（T/TON）。

当9 300 m＜y≤12 000 m时，有气温T=230-0.006 328（y-9 300）+1.172×10-6（y-9 300）2，气压p=0.292 28 pONexp（-2.120 64（arctan（（2.344（y-9 300）-6 328）/32 221）+0.193 925）），空气密度ρ=ρON（p/pON）（T/TON）。

当y＞12 000 m时，气温T=221.5 K，气压p=0.193 72 pONexp（-（y-12 000）/6 483.3），空气密度ρ=ρON（p/pON）（T/TON）。

（3）气象条件的修正。假如只考虑气象条件对阻力函数K的影响。随着弹丸所在位置的海拔高度的增加，ρ值减小，K值减小。空气温度T升高时，声速c随之增大，K值也增大，而气温变高后，密度ρ减小，K值又会减小。根据外弹道理论，可以计算出气温T1引起的K值的相对偏差δ1和空气密度ρ所引起的K值的相对偏差δ2，进而可以用微分法求得K值的相对偏差ΔK对α0的修正量Δα0。同理，可以计算气象条件对其他参数的修正。

2）弹道参数及其修正

弹道条件主要包括弹重m、药温T2及初速v0等。弹重的变化同时影响到初速和弹道系数的变化，从而影响弹头在空气中所受的力和力矩。炮弹火药温度的变化和火炮身管的烧蚀，都将引起初速偏差（均体现为对初速的影响），进而影响基本瞄准角α0。火药温度越高，初速越大，身管烧蚀程度就越深，进而使初速降低。

根据内弹道理论，可以计算出火药温度T2所引起的初速相对偏差δ3、身管烧蚀度N所引起的初速相对偏差δ4、弹重m所引起的初速相对偏差δ4。根据外弹道理论，可以计算出弹重m所引起的阻力函数K值的相对偏差δ5。利用微分法可求出初速偏差Δv0和阻力函数偏差ΔK对α0的修正量Δα0。

3）地形条件及其修正

小射程的射弹弹道受地理条件的影响很小，大射程的射弹弹道需考虑地理条件的影响。考虑地球曲面时，射弹的射程将是射击点到弹着点的弧线长度，同时射弹将受由地球自转引起的科氏力作用，科氏力使头弹产生偏移，影响射击效果。标准地理条件：火炮静止时，射击点与目标同在炮口水平面内；火炮俯仰时，身管轴线在同一铅垂面内；重力加速度g≈9.8 m/s2，方向垂直于地平面；不计科氏加速度；地表面为平面。对于地形条件，主要考虑射击点与弹着点是否在同一水平面上，射击区内有无遮蔽顶等。假设目标高H=0，即炮目高低角ε=0时，基本瞄准角为α0，若距离D相同，但存在炮目高低角ε时的α如图10.7所示。根据外弹道学理论，按求差法，炮目高低角ε对α0的修正量Δα0=α0（cosε-1）。

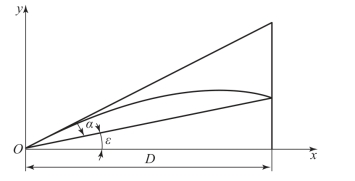
图10.7　对炮目高低角ε的修正

通常，火控系统是在平行于地球平面的坐标内求解弹道方程的。当武器载体侧倾时，火炮相对耳轴或炮塔座圈的任何转动都会同时在其他两个方向上产生角位移效果。为了以地球坐标系为基准，按α和β装定火炮，就必须对火炮在炮塔坐标系内相应的转动角度αt和βt进行计算。它的实质是坐标系进行侧倾角Ψ角转移的坐标变换问题，但在火控系统中仍将其视为修正量计算，而且是一个备受重视的修正问题。

4）炮口偏移及其修正

许多试验结果表明，炮口的空间角度可以从它预先设定的方向发生明显的偏移，主要因素有：火炮身管受热不均匀所导致的身管弯曲；载体运动所产生的振动；射击时所产生的身管振动；等等。对炮口角偏移的修正是颇受重视的一项修正，虽可按射表中给出的跳角γ进行修正，但在先进的火控系统中常采用人工（或自动）直接修正法以及自动间接修正法。直接法是在测得角偏移量后直接校准火炮轴线，保持几何零位。间接法则进一步考虑身管的振动，以统计经验法为基础提出某经验公式进行修正。