学习DSN权值的优化方法

本节我们提供一些关于如何借助DSN线性输出单元来学习DSN权值的技术细节。为简单起见，我们使用一个模块来说明线性输出单元的优势。首先，如果在所有训练数据中的所有隐层的激励矩阵H都已经得到，那么高层的权值矩阵U很容易求出。我们使用向量组X=[x₁，…，x_i，…，x_N]表示训练向量，其中每一个向量x_i=[x_1i，…，x_ji，…，x_Di]^T是关于模块的函数，D表示输入向量的维数，N是训练数据的总数。L表示隐单元的数量，C表示输出向量的维数，一个DSN模块的输出为y_i=U^Th_i，其中h_i=σ（W^Tx_i）是第i个样本的隐层向量，U是一个L×C的上层权值矩阵，W是一个D×L的下层权值矩阵，σ（·）是一个sigmoid函数。如果x_i和h_i中都增加常数1，那么偏置项也隐含在公式中。

用T=[t₁，…，t_i，…，t_N]表示所有训练数据（总共N个样本）的标签，其中t_i=[t_1i，…，t_ji，…，t_Ci]^T，参数U和W通过最小化均方误差得到：

其中网络的输出为

y_i=U^Th_i=U^Tσ（W^Tx_i）=G_i（U，W）

如标准的神经网络一样，输出取决于权值矩阵。假设H=[h₁，…，h_i，…，h_N]已知，或者W已知，令误差函数关于U的导数为0，求得

U=（HH^T）-1HT^T=F（W），

式中，h_i=σ（W^Tx_i）。也就是说，在U和W之间存在一个很明确的约束：在传统的反向传播算法中，U和W是相互独立的。(www.xing528.com)

给定等式约束U=F（W）后，使用拉格朗日乘子法（Lagrangian multiplier method）学习最优化参数W。优化拉格朗日算子为

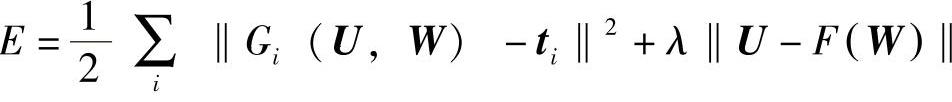
我们得到批量梯度下降算法，而梯度采用下面的形式[106，413]：

式中，H†=H^T（HH^T）-1是H的伪逆（pseudo-inverse），符号表示按元素的成对相乘（element-wise multiplication）。

和传统的反向传播算法相比，因为有明确的约束U=F（W），所以上述方法在梯度计算时噪声较少。经验发现，不同于传统的反向传播，这里使用批量训练可以有效的帮助DSN进行并行学习。