受限玻尔兹曼机的CD-1采样算法及进展

受限玻尔兹曼机（Restricted Boltzmann Machines，RBM）是一种特殊的马尔可夫随机场（Markov Random Filed，MRF）。一个RBM包含一个由随机的隐单元构成的隐层（一般是伯努利分布）和一个由随机的可见（观测）单元构成的可见（观测）层（一般是伯努利分布或高斯分布）。RBM可以表示成双向图，所有可见单元和隐单元之间都存在连接，而隐单元两两之间和可见单元两两之间不存在连接，也就是层间全连接，层内无连接。

一个RBM中，v表示所有可见单元，h表示所有隐单元，给定模型参数θ，可见单元和隐单元的联合概率分布p（v，h；θ）用能量函数E（v，h；θ）定义为

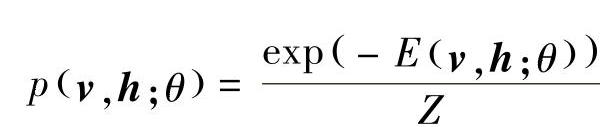
式中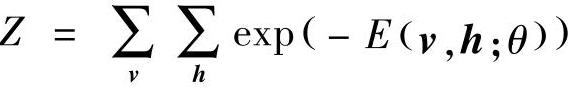，是一个归一化因子或配分函数（partition function），模型关于可见向量v的边缘分布为

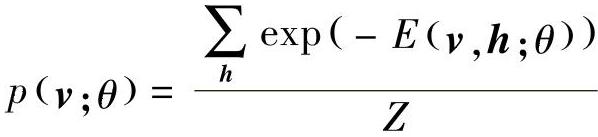
对于一个伯努利（可见单元）分布-伯努利（隐单元）分布的RBM，能量函数的定义为

式中，w_ij表示可见单元v_i和隐单元h_j之间的对称连接权值，b_i和a_j表示偏置项，I和J是可见单元和隐单元的数目。条件概率可以通过下列公式计算：

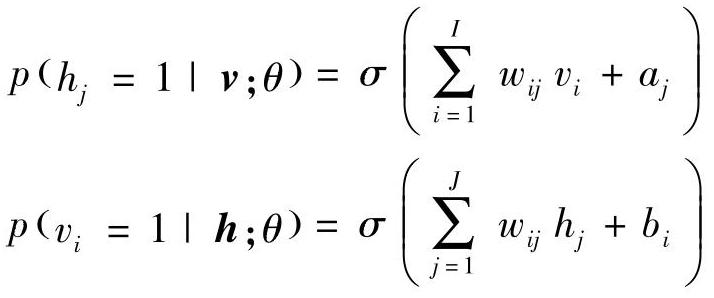
式中，σ（x）=1/（1+exp（-x））。

相似地，对于一个高斯（可见单元）分布-伯努利（隐单元）分布RBM，能量函数为

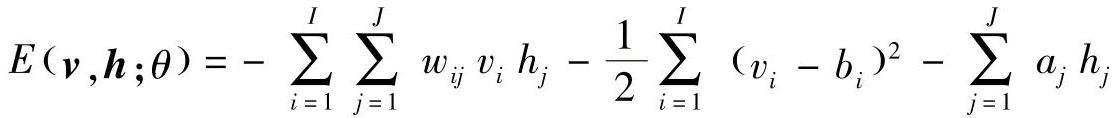
相应地，条件概率为

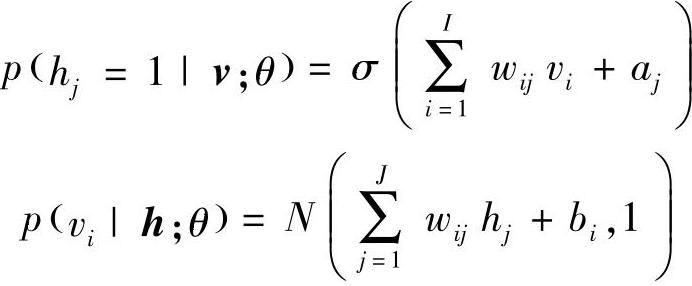
式中，v_i取实值，服从均值为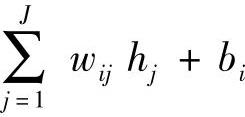，方差为1的高斯分布。高斯-伯努利RBM可以将实值随机变量转换成二进制随机变量，然后使用伯努利-伯努利RBM进行进一步的处理。

上面讨论了RBM中可见变量的两种常见的分布形式——高斯分布（连续变量数据）和二项分布（二进制数据），更一般的分布也可以应用在RBM中。例如，文献[386]中使用了一般的指数族分布。

通过计算对数似然logp（v；θ）的梯度我们可以得到RBM权值更新的公式：(www.xing528.com)

Δw_ij=E_data（v_ih_j）-E_model（v_ih_j），

式中，E_data（v_ih_j）是训练集中观测数据的期望（h_j是在给定v_i之后在模型上采样得到的），E_model（v_ih_j）则是在模型所确定的分布上的期望。然而E_model（v_ih_j）的计算是非常复杂的，使用对比散度（Contrastive Divergence，CD）来近似地计算梯度是一种有效近似期望值的方法，对比散度方法通过由训练数据初始化的吉布斯采样器来代替E_model（v_ih_j），近似计算E_model（v_ih_j）的步骤总结如下：

• 使用训练数据初始化v₀

• 采样h₀～p（h|v₀）

• 采样v₁～p（v|h₀）

• 采样h₁～p（h|v₁）

（v₁，h₁）是从模型中采样得到的，是对E_model（v_ih_j）的一个粗略估计。使用（v₁，h₁）来估计E_model（v_ih_j）促使了CD-1算法的产生，采样算法过程如图5.1所示。

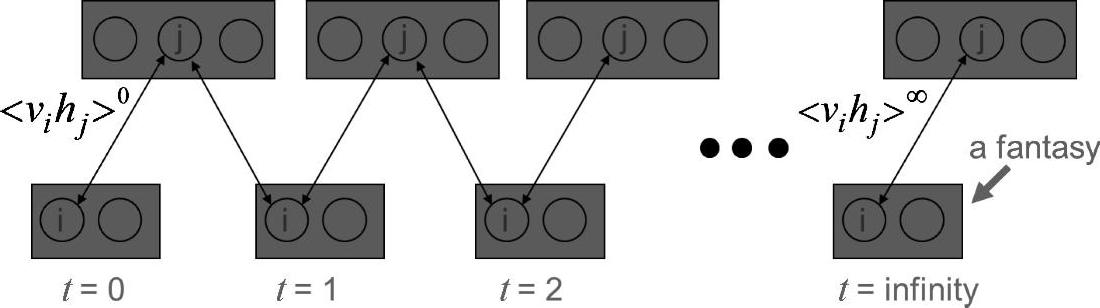
图5.1 RBM学习中采样过程图示（Geoff Hinton的贡献）

图中词语翻译对照表

CD-k算法将CD-1算法进行了推广，即在马尔可夫链上执行多步。当然还有其他方法用来估计RBM的对数似然梯度，如随机最大似然（maximum likelihood）或持续对比散度（Persistent Contrastive Divergence，PCD）^[363，406]。如果将RBM当作生成模型（generative model）使用时，随机最大似然方法和PCD方法会比CD方法的效果要好。

RBM的训练是成功应用RBM的关键，同时也是使用深度学习技术解决实际问题的关键。Hinton在2010年的技术报告[159]中提出了一个非常有助于RBM训练的指南。

以上讨论的RBM既是一个生成模型，也是一个无监督模型，因为它使用隐变量来描述输入数据的分布，而这个过程却没有涉及数据的标签信息。然而，当有可利用的标签信息时，标签信息可以和数据一起使用，组成“联合数据集”，然后使用CD算法来生成与数据相关的近似的“生成”目标函数。另外，还可以定义一个关于标签的条件似然的“判别式”目标函数。判别式RBM可应用于分类任务中的参数微调^[203]。

Ranzato等人在文献[297，295]中提出了一种称为“对称稀疏编码机”（Sparse Encoding Symmetric Machine，SESM）的无监督学习算法。SESM和RBM非常相似，它们都具有对称的编码器和解码器，在编码器的顶层都是一个逻辑非线性（Logistic Non-linearity）结构。主要的区别是RBM的训练使用了（近似）最大似然，而SESM则是简单地通过最小化平均能量加上一个稀疏编码项。SESM使用稀疏项来避免平滑的能量平面，而RBM则是在损失中使用一个明确的对比项，即对数配分函数的一个近似，来达到这个目标。另外一个不同点是，在编码策略上，RBM中的编码单元是“有噪声”的和二进制的，而SESM的编码单元是二进制并且稀疏的。对于语音识别任务，在预训练DNN过程中使用SESM的例子可参见文献[284]。